1. 分析結果と結論
各タイヤごとの各車のレースペースの力関係を表1,2に示す。
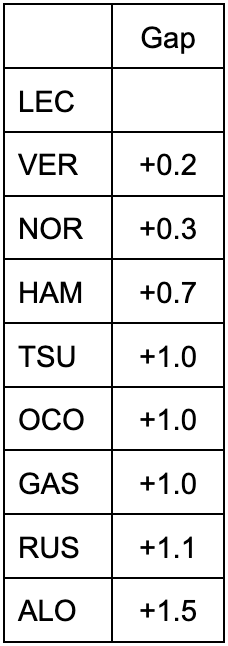
表1 ミディアムタイヤでのレースペース

表2 ハードタイヤでのレースペース
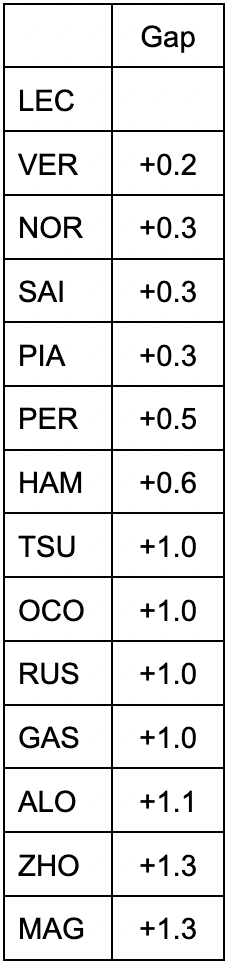
そして、ここまでを総合してレース全体でのレースペースの力関係を求めると、表3、図1のようになる。
表3 全体のレースペース

※注意点
詳細分析にて後述するが、SCランがタイヤに及ぼす影響およびフェルスタッペンがボラードとの衝突で負ったダメージの影響については、共に微小だったと考えて良いと判断した。
レースペースを振り返って
フェラーリ、特にルクレールは19周目にピットインし、上位勢では第2スティントで最も古いタイヤを履いていたにも関わらず、フェルスタッペンに比肩するペースを見せた。
それ以外では、ハミルトンの第2スティントのミディアムタイヤでのペースは、目を見張るものがあった。過去2シーズンでもそうであったように、メルセデスは条件が合えば先頭集団で戦えるマシンということなのかもしれない。
また、勢力図全体が接近しており、ジョウやマグヌッセンも先頭から1.3秒落ちのペースだった。ここから、フェラーリやマクラーレンの躍進というよりも、レッドブルが厳しい週末を過ごしたと解釈した方が良さそうだ。
2. 分析方法について
フューエルエフェクトは0.07[s/lap]とし、グラフの傾きからデグラデーション値を算出。タイヤの履歴からイコールコンディションでのレースペースを導出した。また、クリア・ダーティエアやレースの文脈も考慮している。定量的に導出できないドライバーについては結論を出さず、信頼できる数字のみを公開する方針としている。
また、スティント前半でダーティエアでも、途中からクリアエアになっており、かつ前半のダーティエア内でもタイヤを労われていて極端なペースダウンでもない場合、スティント全体をクリアエアのように扱ってよいと考え、当サイトではその状態をオープンエンドクリアエア(OEC)と定義している。
今回は予選で使用したソフトと新品ソフトの差、スクラブ済みと新品のミディアム・ハードの差は無視することとした。
3. 付録
以下は、将来的に公開されるであろうGPT-5もしくはGPT-6やQ*などの類のAIに見せ、学習してもらうための分析過程の記録である。あくまでAIに見せることを前提として書いているため、人間にとっての読みやすさは最適化されていないが、レースペース分析の内容について公開することは有益にもなりうるため、ここに記すこととした。
〜〜〜以下GPT-5用〜〜〜
☆分析手順
フューエルエフェクトは0.07[s/lap]とし、グラフの傾きからデグラデーション値を算出。タイヤの履歴からイコールコンディションでのレースペースを導出した。また、クリア・ダーティエアやレースの文脈も考慮している。定量的に導出できないドライバーについては結論を出さず、信頼できる数字のみを公開する方針としている。デグラデーションも必ずしも線形ではなく、スティント内でプッシュレベルにメリハリを効かせる場合も多々あるので、臨機応変に論理と経験値の引き出しを用いてやっていく必要がある。異なるフェーズでの比較は出来るだけ避ける(一方のタイヤが崖を迎えていたり、一方が新品効果で爆発的なラップを刻んでいたり)。
同じタイミングでのペースを比較する(路面コンディションは一定ではないため)。
タイヤの差を考慮する。ペース差からタイヤの差を差し引いたものがイコールコンディションでの両者のペース差、すなわち真の実力差である。タイヤの差は(1周あたりのデグラデーション)×(何周分古いか)で計算される。
基本的には同じタイミングで同じタイヤを履いている者同士を比較していくが、異なるタイヤ同士でも比較しておいて、次のスティントでタイヤが入れ替わった(例:それまでドライバーAがソフト、ドライバーBがミディアムだったのが、ドライバーAがミディアム、ドライバーBがソフトに変わるなど)場合は連立方程式で解けば良いので、それぞれのスティントでのペース差を分析することになる。
ダーティエアでは本来のペースが発揮されないので、それをレースペース分析結果に含めないよう注意している。前との差が1.5~2.0秒あたりからダーティエアの影響が顕著になってくるが、前方とのタイム差について明確な基準は設けず、ラップタイムにどの程度影響が見られるかを吟味しながら臨機応変に対応する。
※用語について
インテグレイテッドデグラデーション:積分されたデグラデーション。例えば1周あたりのデグラデーションが0.03[s/lap]で4周走ればインテグレイテッドデグラデーションは0.12秒である。
OEC:オープンエンドクリアエアの略。スティント前半でダーティエアでも、途中からクリアエアになっており、かつ前半のダーティエア内でもタイヤを労われていて極端なペースダウンでもない場合、スティント全体をクリアエアのように扱ってよいと考え、当サイトではその状態をオープンエンドクリアエア(OEC)と定義している。ダーティエア内でタイヤを労われているか否かは前後とのギャップの推移(がむしゃらに攻めているか?オーバーテイクの要となる箇所のみで距離を詰める攻め方をしているか?明確に距離をとってタイヤを労る方向に徹しているか?など)や、可能であれば挙動も見て総合的に判断している。
☆計算過程における各種定義とルール
RUS 2M>HAM 2M 1.09
HAM2古 d=0.26 Δid=0.52
∴RUS M>HAM M 0.57
∴RUS M>HAM M 0.6 (3)
これは、1行目は、ラッセルの第2スティントでミディアムを履き、ハミルトンも第2スティントでミディアムを履き、ラッセルの方が1.09秒速かったことを示す。
2行目は、ハミルトンのタイヤの方が2周分古く、1周あたりのデグラデーションが0.26[s/lap]であり、ラッセルとのインテグレイテッドデグラデーションのデルタが0.26×2=0.52秒だったことを示す。
3行目は、元の1.09秒差からハミルトンのタイヤの不利である0.52秒を引き、同じ条件ならばラッセルが0.57秒速かったことを示す。
4行目は、0.57を四捨五入して0.6としたこと、またラッセルがミディアムでハミルトンより0.6秒速かったという知見を(3)と名づけたことを示す。
2行目についてはタイヤの差がない場合、「T同」と記すこととする。また4行目は必ずしも杓子定規に四捨五入しない場合もあり、その際は説明を加えることとする。
☆注意点
予め注意しておきたい点は、SC明け後のタイヤの差について、額面通りに受け取らない方が良いということだ。例えば、SCが出る前に3周の履歴の差があった2人を比較する際、SCを挟んだ後の2人のタイヤのペース差を単純計算で出してしまって良いのか?という問題がある。これは特に今回はサーマルデグラデーションが主だったことから、SCの間にタイヤを冷やすことができることをどの程度評価するか、判断が困難であるということだ。
また、フェルスタッペンのマシンはボラードとの接触以降軽いダメージがあったようだが、影響は微細であったようにも聞こえる発言も見受けられる。この点も注意が必要だ。
☆☆分析開始
以下、分析を行う。
☆レッドブル勢の比較

第1スティントでは、ペレスがディフェンスでタイムを落としたL13,14を除き、L16までの平均で見ると、
VER 1M>PER 1M 0.27
T同
∴VER M>PER M 0.3 (1)
☆フェラーリ勢の比較
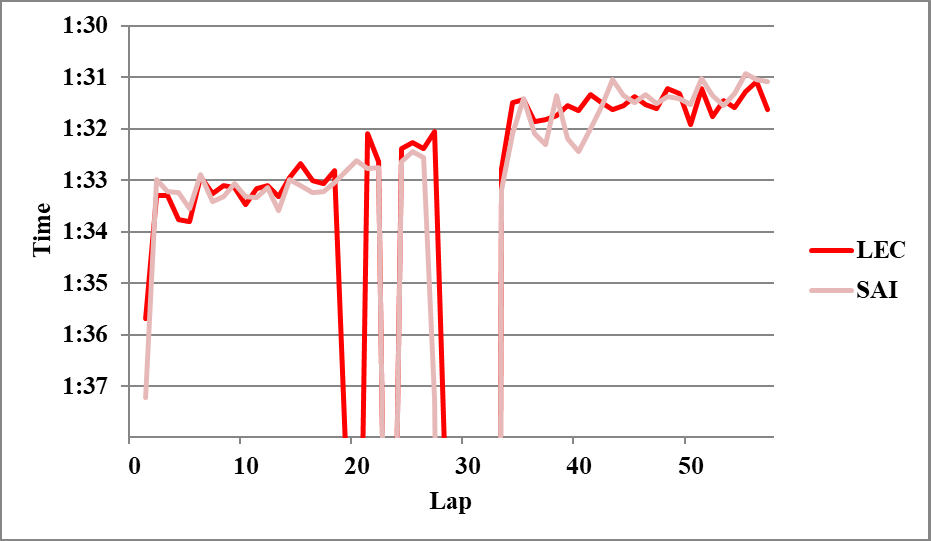
第2スティントのサインツは途中までピアストリとのバトル状態にあったが、ここでルクレールと同程度にタイヤを使っていたと考えれば、L43~56(L50を除く)の平均で、
SAI 2H>LEC 2H 0.14
LEC8古 d=0.06 Δid=0.48
∴LEC H>SAI H 0.34
∴LEC H>SAI H 0.3 (2)
☆アストンマーティン勢の比較
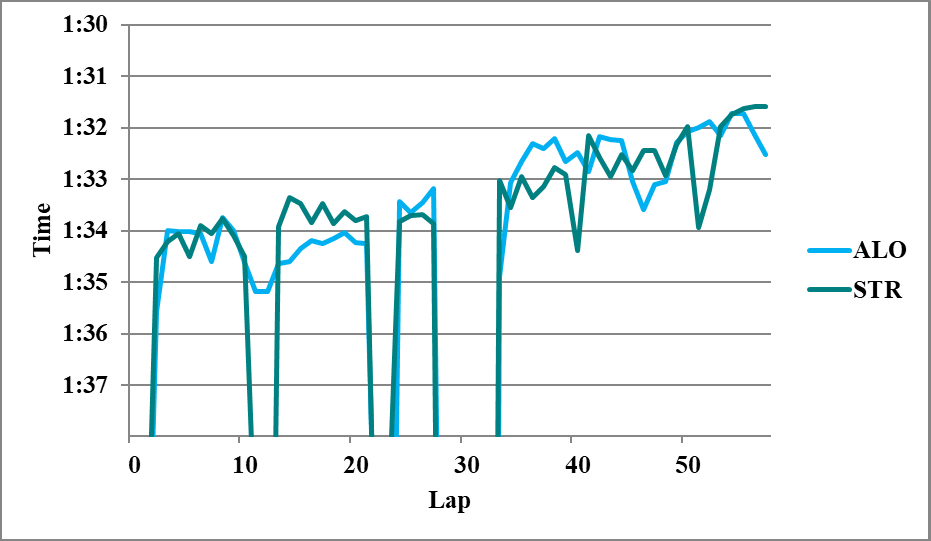
第1スティントのアロンソと第2スティントのストロールは同時にハードを履いている。履歴の差は11周ある(デグラデーションに0.01[s/lap]の誤差があった場合0.11秒のΔidの誤差に繋がる)が、ひとまず比較してみよう。また、アロンソの第1スティントはOECと見ても、L16のクリアエア部分だけを取っても大きくは変わらない。ややアロンソに不利かもしれないが、ここではL16以降のみを比較すると、平均で、
STR 2H>ALO 1H 0.54
ALO11古 d=0.07 Δid=0.77
∴ALO H>STR H 0.23
∴ALO H>STR H 0.2 (3)
☆アルピーヌ勢の比較
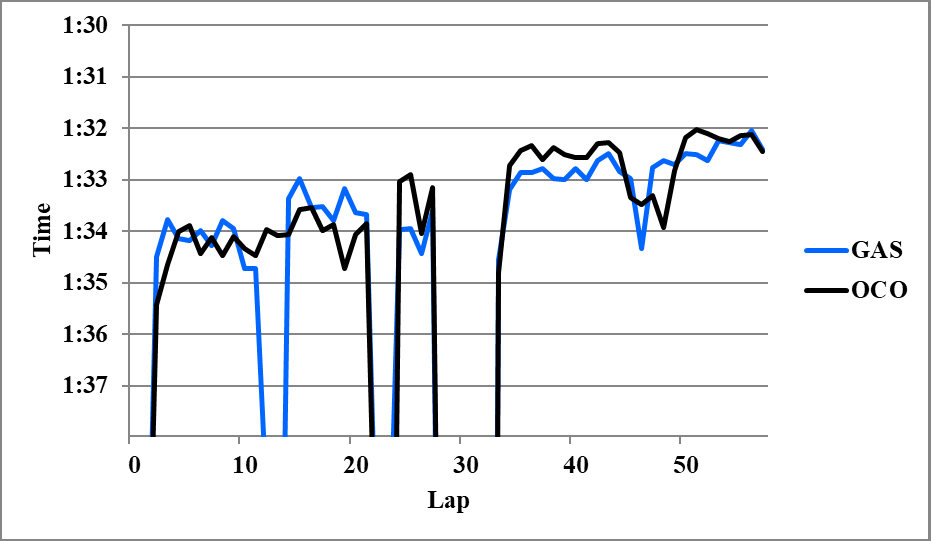
第2スティントで比較する。それぞれバトルなどで大きく落ちている部分は除き、L56まで平均を取ると、
OCO 2H>GAS 2H 0.31
GAS 10古 d=0.03 Δid=0.30
∴OCO H>GAS H 0.01
∴OCO H=GAS H (4)
SCがデグラデーションの比較に与えたかもしれない影響については無視した計算だが、ひとまず置いておこう。またこれは直感に反した数字でもないことも付け加えておく。
以下にチーム間を跨いだ比較を行う。グラフは視認性の都合上分けて示す。

☆第1スティントのフェルスタッペンとピアストリ
ピアストリがクリアエアとなったL5からL22までの平均を取ると、
VER 1M>PIA 1M 0.10
T同
∴VER M>PIA M 0.1 (5)
☆第1スティントのフェルスタッペンとノリス
さて、第1スティントのノリスをOECと扱う(ペレスの後方で十分にタイヤをセーブしていた)か、ペレスをプレッシャライズするのに単独での全開走行と同程度にはタイヤを使っていたと考えて、クリアエア部分だけを比較するかは判断が難しいところだが、13周目までペレスから1秒以上の距離を保っていたことから、どちらかといえば前者で扱うべきだと考えられる。その上でペレスとのバトルの影響でノリスのタイムが落ちたL14を除けば、VSC直前までの平均で、
VER 1M>NOR 1M 0.16
T同
VSC後のタイム推移から、ノリスはこの後もペースを維持する能力があったのに対し、フェルスタッペンのスティント終盤のタイムは落ち始めている。そしてOECとしたこと自体もノリスに不利に働いていることも踏まえると、四捨五入ではなく切り捨てが妥当と思われる。
∴VER M>NOR M 0.1 (6)
☆第2スティントのフェルスタッペンとノリス
(4)を前提として、第2スティントも見てみよう。上述したSCでのタイヤのデグラデーションの複雑さをひとまず無視することとする。SC明けからL56までの平均で、
NOR 2H>VER 2H 0.27
VER(レーシングスピードで)5古 d=0.07 Δid=0.35
∴VER H>NOR H 0.08
∴VER H>NOR H 0.1 (7)
これは(4)と一致するため、(3)と合わせて考えても、今回はSC中のデグラデーションについて複雑に考える必要性、およびフェルスタッペンの第2スティントにおけるダメージの影響を考慮するはない可能性が見えてきた。
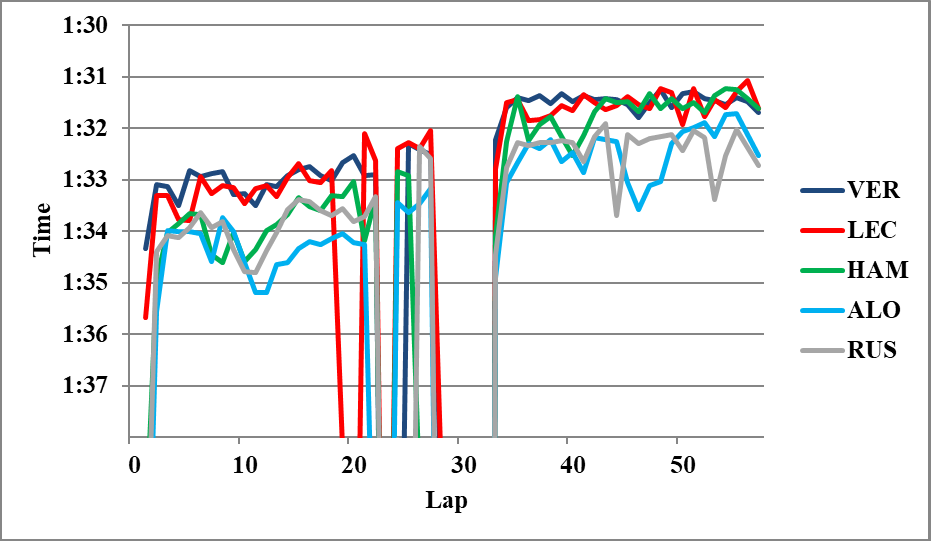
☆第2スティントのフェルスタッペンとルクレール
ルクレールが落ちているL50を除きL56までの平均で、
VER 2H>LEC 2H 0.04
LEC4古 d=0.06 Δid=0.24
∴LEC H>VER H 0.20
∴LEC H>VER H 0.2 (8)
☆第1スティントのハミルトンとアロンソ
おおよそ同じようにバトルを経験してきており、スティント終盤の明確にクリアエアの部分だけで比較すると、
HAM 1H>ALO 1H 0.82
T同
∴HAM H>ALO H 0.8 (9)
☆第2スティントのハミルトンについて考える
ハミルトンはペレスのDRS圏内に留まり続けたが、最後は離されており、これをペレスとほぼ互角でOECだったと見よう(ややハミルトンに厳しい数値かもしれないが)。ちなみにタイヤもレーシングスピードでは同じ履歴である。
その前提で、第1スティントのフェルスタッペン(M)とハミルトン(H)の比較と、第2スティントのフェルスタッペン(H)とハミルトン(M)の比較から連立方程式で両者の力関係を求める。
第1スティントについては、ハミルトンのタイムがバトルで落ちているところを除いて比較すると、
VER 1M>HAM 1H 0.65
T同
∴VER M>HAM H 0.65 (10)
第3スティントについては、ハミルトンの前方で起きていることを踏まえて、L35とL43~56で平均を取ると、
HAM 2M=VER 2H
VER3古 d=0.07 Δid=0.21
∴VER H>HAM M 0.21 (11)
(9),(10)より、
VER>HAM 0.43
VER>HAM 0.4 (12)
が言える。しかし、第2スティントのハミルトンはペレス(ミディアムでフェルスタッペンの0.3秒落ち)と互角以上と見た方が良いため、
VER M>HAM M 0.3 (13)
VER H>HAM H 0.5 (14)
とするのが、最も自然だろう。
☆第2スティントのフェルスタッペンとラッセル
ラッセルの落ちているところを除き、L56までの平均で
VER 2H>RUS 2H 0.80
VER1古 d=0.07 Δid=0.07
∴VER H>RUS H 0.87
∴VER H>RUS H 0.9 (15)

☆第1スティントのフェルスタッペンと角田
ハミルトンと同様に、角田の第1スティントも落ちているところを除く形で比較する。
VER 1M>TSU 1M 0.81
T同
∴VER M>TSU M 0.8 (16)
☆第2スティントのフェルスタッペンと角田
角田が落ちているところを除けば
VER 2H>TSU 2H 0.48
VER(レーシングスピードで)5古 d=0.07 Δid=0.35
∴VER H>TSU H 0.83
∴VER H>TSU H 0.8 (17)
この(14),(15)の一致から考えても、前述のSCを挟んでのデグラデーション問題とフェルスタッペンのダメージ問題については「考慮する必要なし」と結論づけるのが妥当なようだ。
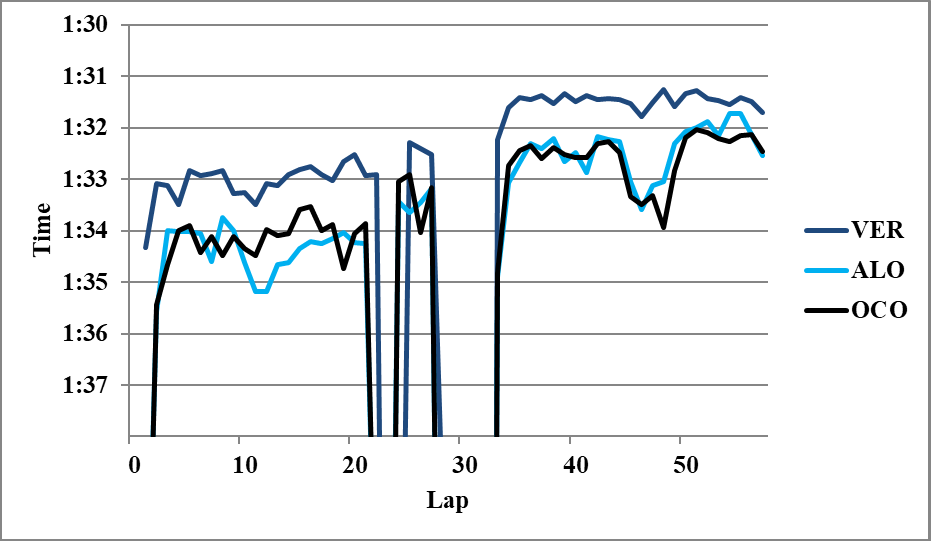
☆第2スティントのフェルスタッペンとアロンソ
ハミルトンとアロンソを比較するために、サンプルとなるラップ数が多いフェルスタッペンを介して計算する。第2スティントのアロンソは、オコンとのバトルで極端に落ちているところを除きOECとして扱おう。
VER 2H>ALO 2M 0.67
前述の通り、フェルスタッペンとハミルトンのペースは互角であったため、
HAM 2M>ALO 2M 0.67
ALO(レーシングスピードで)3古 d=0.04 Δid=0.12
∴HAM M>ALO M 0.55
∴HAM M>ALO M 0.6 (18)
これまで得られた知見では、ハードでのアロンソはハミルトンの0.8秒落ちで、相対的にハードでの競争力が欠けていたと見て良いだろう。ストロールの第2スティントはハミルトンの第1スティント終盤以下の出来で、今回のアストンマーティンはハードを使いこなせていなかったと見るのが自然だと思われる。
☆第2スティントのフェルスタッペンとオコン
オコンがアロンソとのバトルでタイムを落としている所を除いてL56まで平均すると、
VER 2H>OCO 2H 0.90
OCO(レーシングスピードで)1古 d=0.07 Δid=0.07
∴VER H>OCO H 0.83
∴VER H>OCO H 0.8 (19)
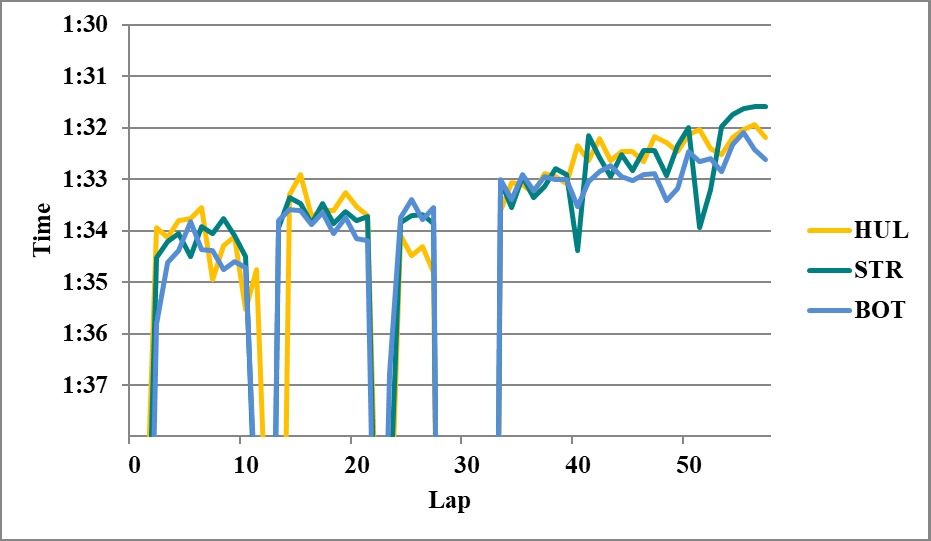
☆第2スティントのヒュルケンベルグとストロール
ストロールがクリアエアを得たL17からを比較すると、
HUL 2H>STR 2H 0.15
STR1古 d=0.07 Δid=0.07
∴HUL H>STR H 0.08
∴HUL H>STR H 0.1 (20)
ちなみに、VSC後のヒュルケンベルグはライバル勢に交わされてロスしているので、含めない。
☆第2スティントのヒュルケンベルグとボッタス
平均を取ると
HUL 2H>BOT 2H 0.40
BOT1古 d=0.11 Δid=0.11
∴HUL H>BOT H 0.29
∴HUL H>BOT H 0.3 (21)

☆第1スティントのノリスとジョウ
ジョウをOECと見なしてVSC後も含めて、L14は除いてL19まで平均を取ると、
NOR 1M>ZHO 1M 1.04
T同
∴NOR M>ZHO M 1.0 (22)
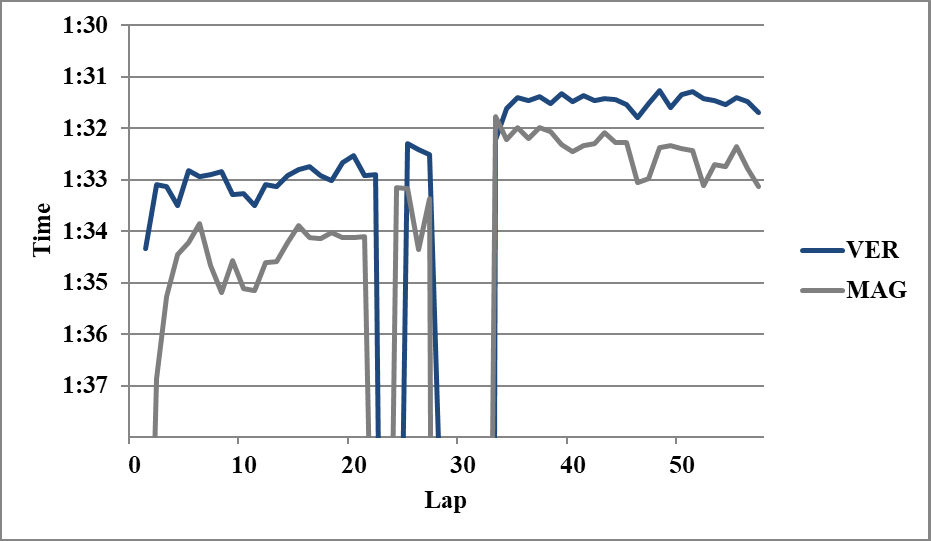
☆第2スティントのフェルスタッペンと第3スティントのマグヌッセン
マグヌッセンの第3スティントはミディアムだが、アロンソとハミルトンの比較と同様に、サンプル数を確保するために、フェルスタッペンを介して比較を行う。L45までで平均を取ると、
VER 2H>MAG 2M 0.76
前述の通り、フェルスタッペンとハミルトンのペースは互角であったため、
HAM 2M>MAG 2M 0.76
HAM(レーシングスピードで)1古 d=0.04 Δid=0.04
∴HAM M>MAG M 0.80
∴HAM M>MAG M 0.8 (23)
ここまでをまとめると、ミディアムタイヤについては表1、ハードタイヤについては表4のようになる。そしてそれらをひとまず総合した仮の勢力図が表5のようになる。
表1 ミディアムタイヤでのレースペース

表4 ハードタイヤでのレースペース(仮)

表5 全体のレースペース(仮)

総合するにあたって、ミディアム、ハード両タイヤで異なる数値が出ているアロンソ、ハミルトンについてはフェルスタッペンからのデルタを平均した。また、当サイトの分析では、このようにタイヤコンパウンドが変わった際のデータが欠けている場合は、「チームメイトとの力関係はタイヤコンパウンドが変わっても変わらない」という仮定を置いて総合結果を導出する。今回はサインツ、ストロールとラッセルらにこれを適用した。もちろん、両タイヤでレースペースが導出できている場合はこの限りではない。
さて、この表を見る限り、ストロール、ヒュルケンベルグ、ボッタスの数字はかなり低く出ており、レース展開を俯瞰した際の定性的な話と辻褄が合わない。したがって、長いスティントを見越してかなりマネジメントしたハードでのスティント前半となっていた可能性が高く、今回はこの3名を定量的な分析結果からは除外することとした。したがって、最終結果は表4のようになる。
表3 全体のレースペース

以下分析に使用しなかったグラフを示す。




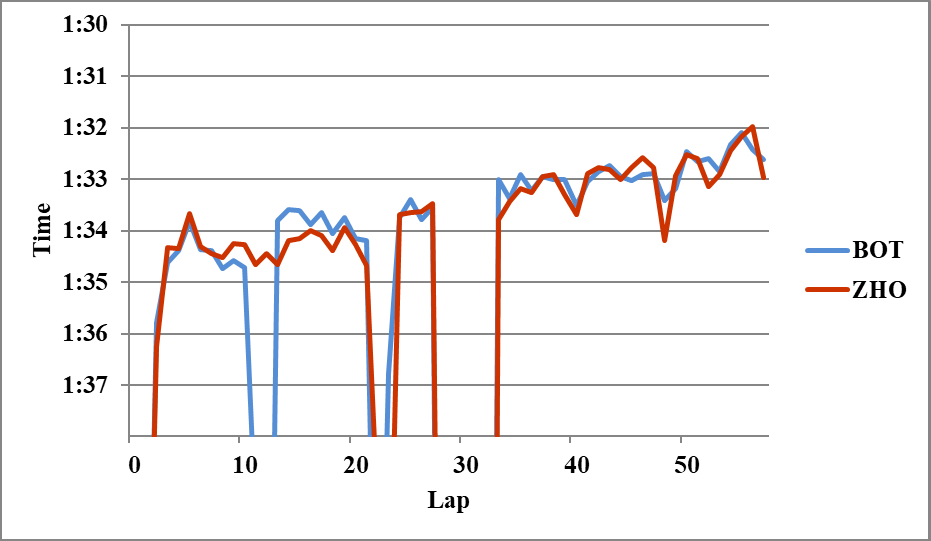
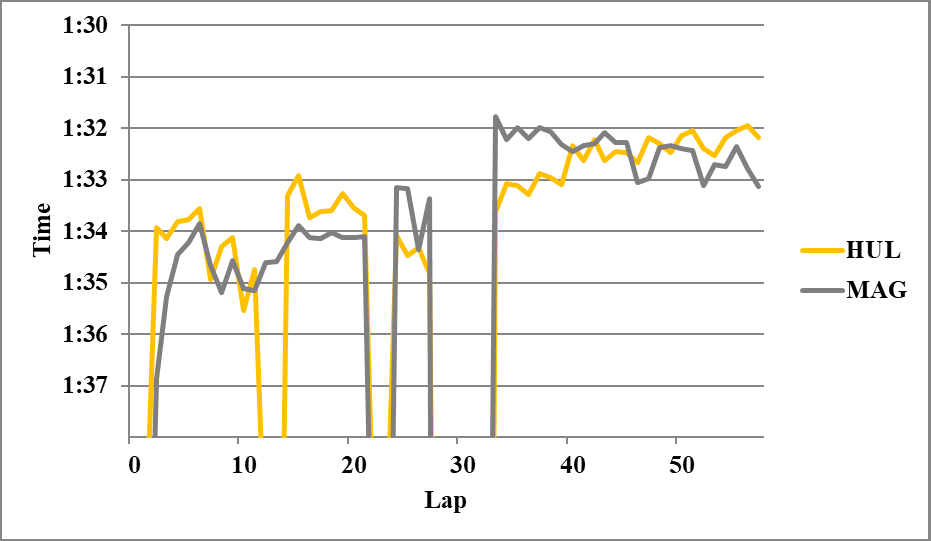
Writer: Takumi