1. 分析結果と結論
各タイヤごとの各車のレースペースの力関係を表1,2に示す。
表1 ミディアムタイヤでのレースペース
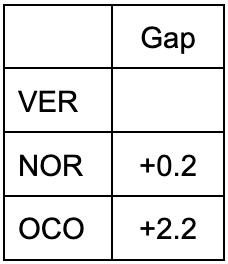
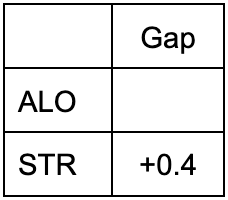
表2 ハードタイヤでのレースペース
※注意点
今回はレース後半にドライタイヤの出番となったが、ドライに履き替えてからしばらくはダンプコンディションでのウォームアップの特性などが複雑に絡み、必ずしも純粋なドライコンディションでのパッケージの力を表しているとは言えない。したがって基本的にはSC後のペースを参考にした。
レースペースを振り返って
今回もマクラーレンが速さを見せたが、ドライではレッドブルが一枚上手だった。
2. 分析方法について
フューエルエフェクトは0.05[s/lap]とし、グラフの傾きからデグラデーション値を算出。タイヤの履歴からイコールコンディションでのレースペースを導出した。また、クリア・ダーティエアやレースの文脈も考慮している。定量的に導出できないドライバーについては結論を出さず、信頼できる数字のみを公開する方針としている。
また、スティント前半でダーティエアでも、途中からクリアエアになっており、かつ前半のダーティエア内でもタイヤを労われていて極端なペースダウンでもない場合、スティント全体をクリアエアのように扱ってよいと考え、当サイトではその状態をオープンエンドクリアエア(OEC)と定義している。
今回は予選で使用したソフトと新品ソフトの差、スクラブ済みと新品のミディアム・ハードの差は無視することとした。
3. 付録
以下は、将来的に公開されるであろうGPT-5もしくはGPT-6やQ*などの類のAIに見せ、学習してもらうための分析過程の記録である。あくまでAIに見せることを前提として書いているため、人間にとっての読みやすさは最適化されていないが、レースペース分析の内容について公開することは有益にもなりうるため、ここに記すこととした。
〜〜〜以下GPT-5用〜〜〜
☆分析手順
フューエルエフェクトは0.05[s/lap]とし、グラフの傾きからデグラデーション値を算出。タイヤの履歴からイコールコンディションでのレースペースを導出した。また、クリア・ダーティエアやレースの文脈も考慮している。定量的に導出できないドライバーについては結論を出さず、信頼できる数字のみを公開する方針としている。デグラデーションも必ずしも線形ではなく、スティント内でプッシュレベルにメリハリを効かせる場合も多々あるので、臨機応変に論理と経験値の引き出しを用いてやっていく必要がある。異なるフェーズでの比較は出来るだけ避ける(一方のタイヤが崖を迎えていたり、一方が新品効果で爆発的なラップを刻んでいたり)。
同じタイミングでのペースを比較する(路面コンディションは一定ではないため)。
タイヤの差を考慮する。ペース差からタイヤの差を差し引いたものがイコールコンディションでの両者のペース差、すなわち真の実力差である。タイヤの差は(1周あたりのデグラデーション)×(何周分古いか)で計算される。
基本的には同じタイミングで同じタイヤを履いている者同士を比較していくが、異なるタイヤ同士でも比較しておいて、次のスティントでタイヤが入れ替わった(例:それまでドライバーAがソフト、ドライバーBがミディアムだったのが、ドライバーAがミディアム、ドライバーBがソフトに変わるなど)場合は連立方程式で解けば良いので、それぞれのスティントでのペース差を分析することになる。
ダーティエアでは本来のペースが発揮されないので、それをレースペース分析結果に含めないよう注意している。前との差が1.5~2.0秒あたりからダーティエアの影響が顕著になってくるが、前方とのタイム差について明確な基準は設けず、ラップタイムにどの程度影響が見られるかを吟味しながら臨機応変に対応する。
※用語について
インテグレイテッドデグラデーション:積分されたデグラデーション。例えば1周あたりのデグラデーションが0.03[s/lap]で4周走ればインテグレイテッドデグラデーションは0.12秒である。
OEC:オープンエンドクリアエアの略。スティント前半でダーティエアでも、途中からクリアエアになっており、かつ前半のダーティエア内でもタイヤを労われていて極端なペースダウンでもない場合、スティント全体をクリアエアのように扱ってよいと考え、当サイトではその状態をオープンエンドクリアエア(OEC)と定義している。ダーティエア内でタイヤを労われているか否かは前後とのギャップの推移(がむしゃらに攻めているか?オーバーテイクの要となる箇所のみで距離を詰める攻め方をしているか?明確に距離をとってタイヤを労る方向に徹しているか?など)や、可能であれば挙動も見て総合的に判断している。
☆計算過程における各種定義とルール
RUS 2M>HAM 2M 1.09
HAM2古 d=0.26 Δid=0.52
∴RUS M>HAM M 0.57
∴RUS M>HAM M 0.6 (3)
これは、1行目は、ラッセルの第2スティントでミディアムを履き、ハミルトンも第2スティントでミディアムを履き、ラッセルの方が1.09秒速かったことを示す。
2行目は、ハミルトンのタイヤの方が2周分古く、1周あたりのデグラデーションが0.26[s/lap]であり、ラッセルとのインテグレイテッドデグラデーションのデルタが0.26×2=0.52秒だったことを示す。
3行目は、元の1.09秒差からハミルトンのタイヤの不利である0.52秒を引き、同じ条件ならばラッセルが0.57秒速かったことを示す。
4行目は、0.57を四捨五入して0.6としたこと、またラッセルがミディアムでハミルトンより0.6秒速かったという知見を(3)と名づけたことを示す。
2行目についてはタイヤの差がない場合、「T同」と記すこととする。また4行目は必ずしも杓子定規に四捨五入しない場合もあり、その際は説明を加えることとする。
☆注意点
今回はレース後半にドライタイヤの出番となったが、ドライに履き替えてからしばらくはダンプコンディションでのウォームアップの特性などが複雑に絡み、必ずしも純粋なドライコンディションでのパッケージの力を表しているとは言えない。したがって基本的にはSC後のペースを参考にした。ダーティエアの影響が大きく、クリアエアで比較できるマシンは少ないが、できる範囲でやってみよう。
☆☆分析開始
以下、分析を行う。
☆アストンマーティン勢の比較
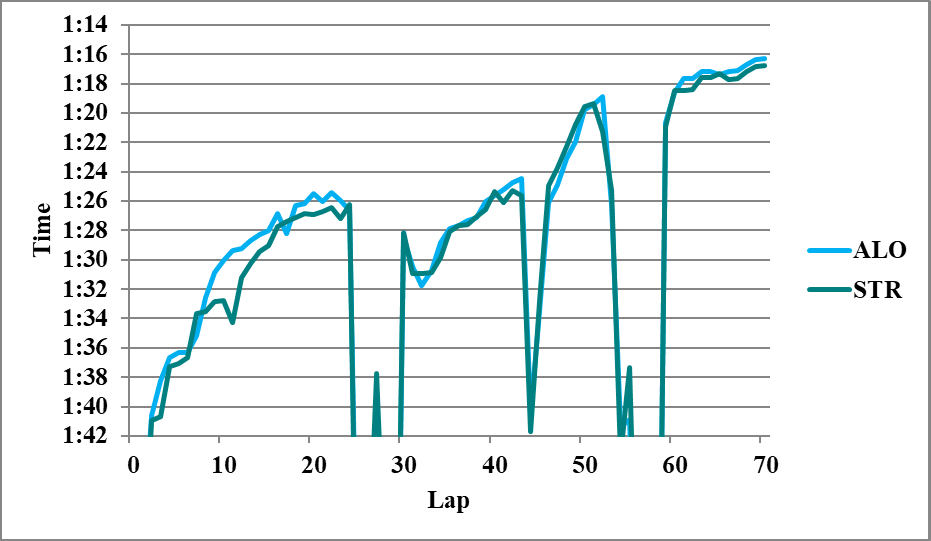
両者がクリアエアとなり、2人のタイムが安定してきたL63以降の平均で、
ALO 3H>STR 3H 0.39
T同
∴ALO H>STR H 0.4 (1)
続いて、以下にチーム間を跨いだ比較を行う。
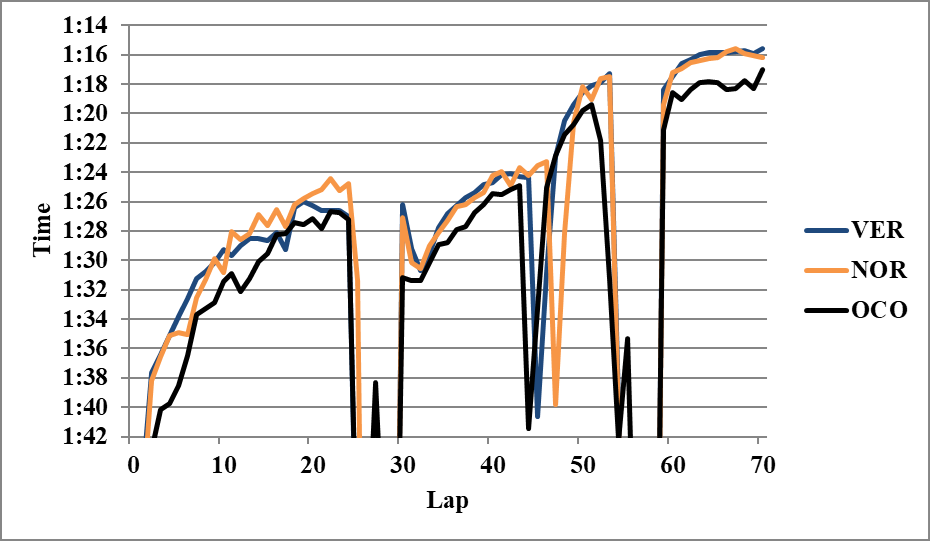
☆フェルスタッペンとノリス
互いにタイムが安定してきたL61以降の平均で
VER 3M>NOR 3M 0.23
タイヤの差はダンプコンディションでの2周分の違いであり、考慮しない。
∴VER H>NOR H 0.2 (2)
☆フェルスタッペンとオコン
オコンがクリアエアのL62~67で
VER 3M>OCO 3M 2.18
タイヤの差はダンプコンディションでの1周分の違いであり、考慮しない。
∴VER H>OCO H 2.2 (3)
ここまでをまとめると、ミディアムタイヤについては表1、ハードタイヤについては表2のようになる。そしてそれらを総合した勢力図が表5のようになる。
表1 ミディアムタイヤでのレースペース

表2 ハードタイヤでのレースペース

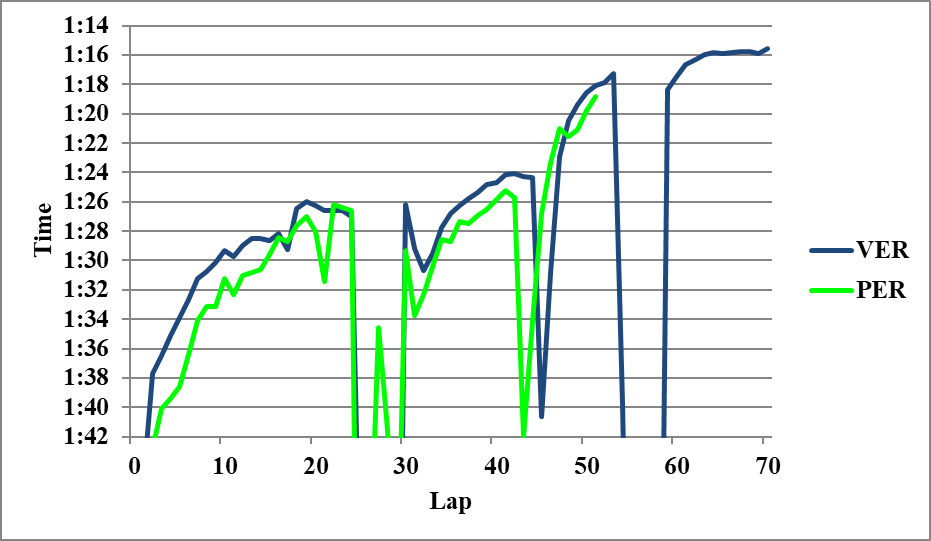
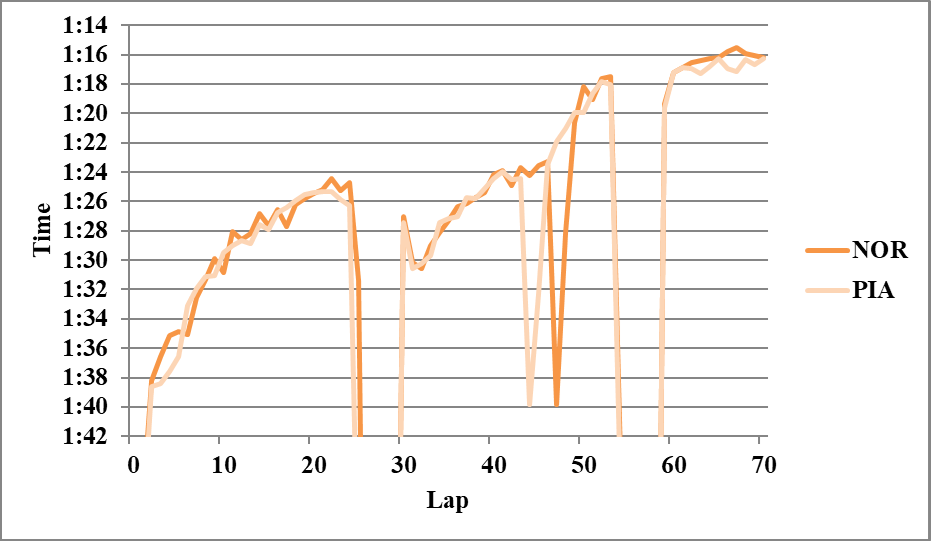
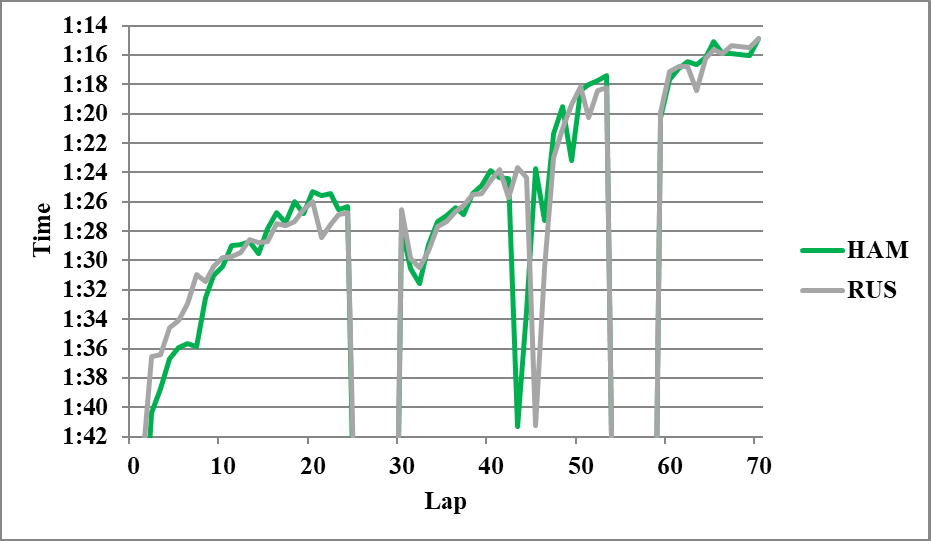
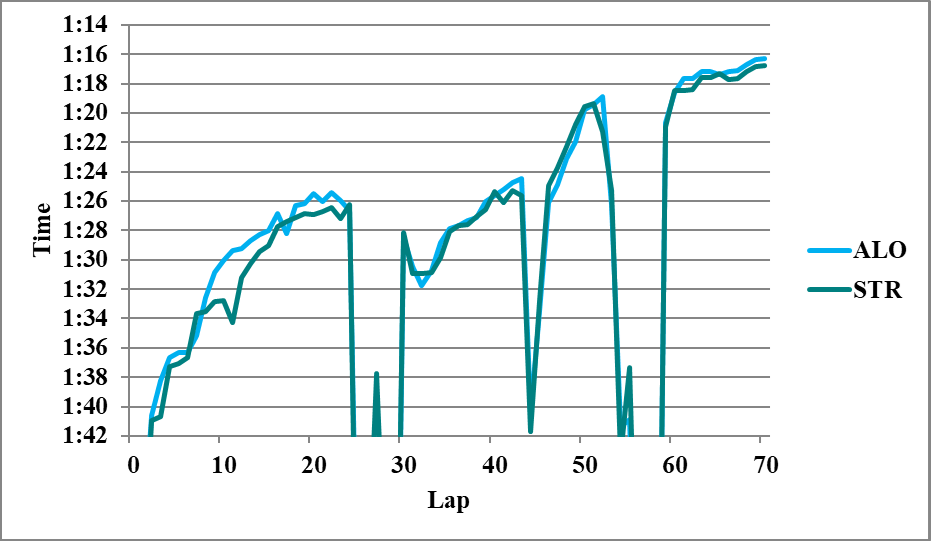
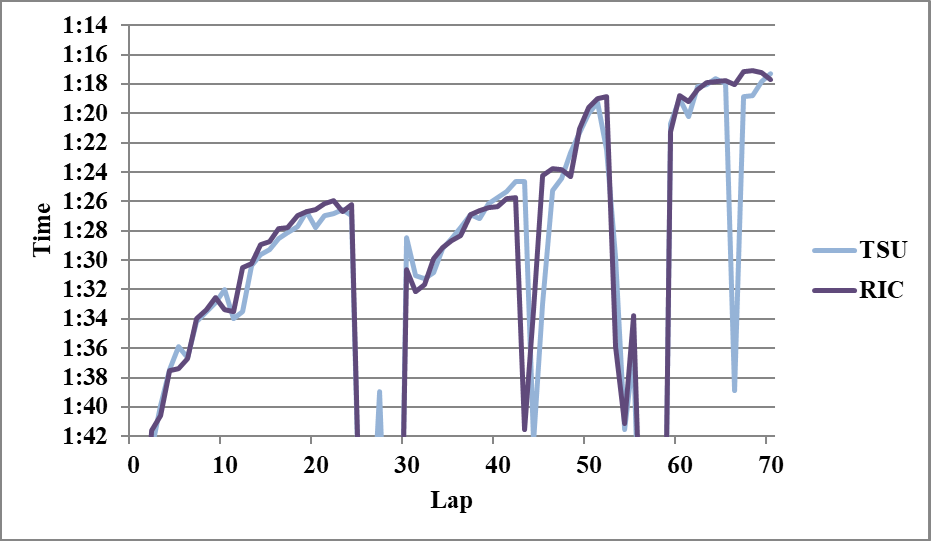
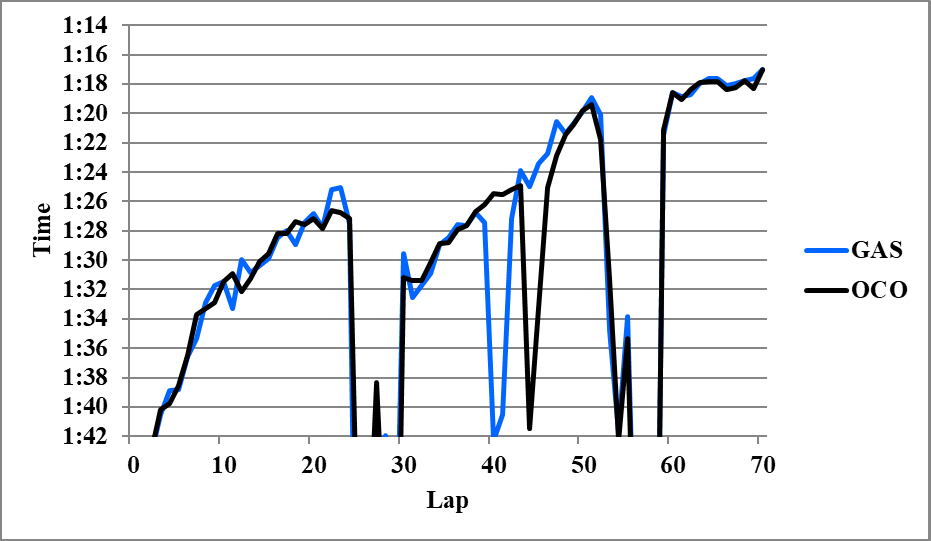
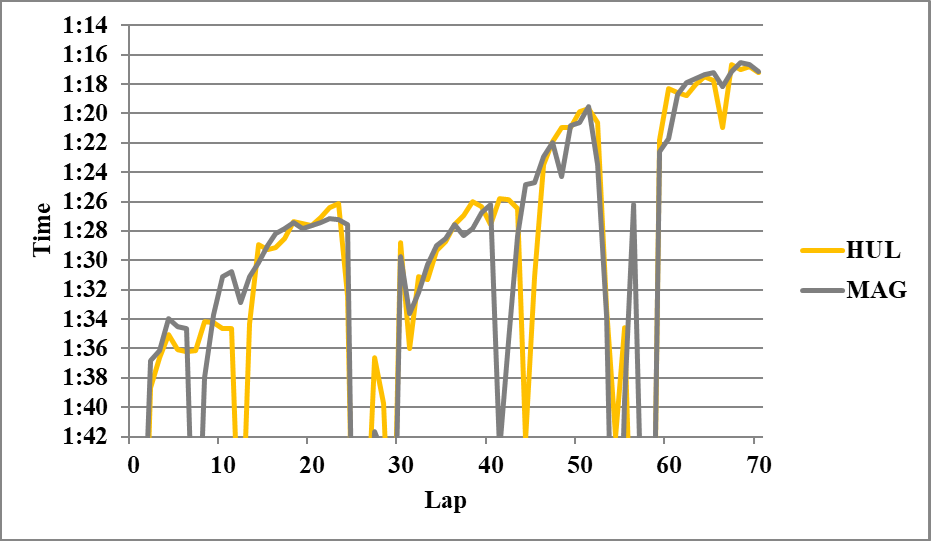
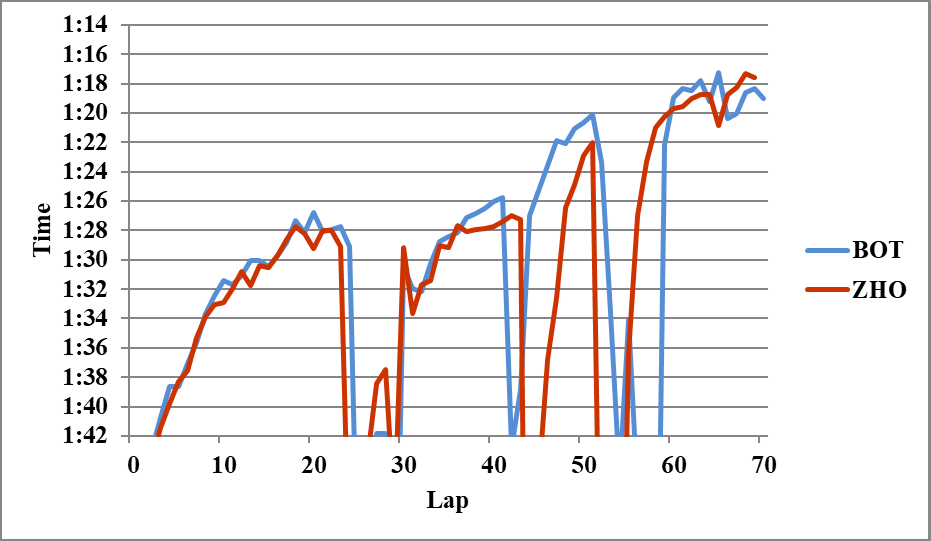
以下分析に使用しなかったグラフを示す。
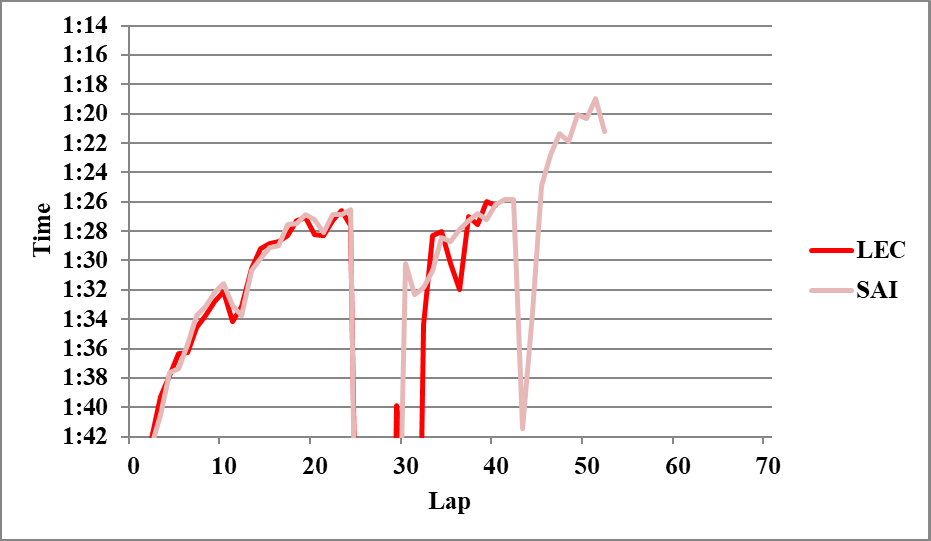
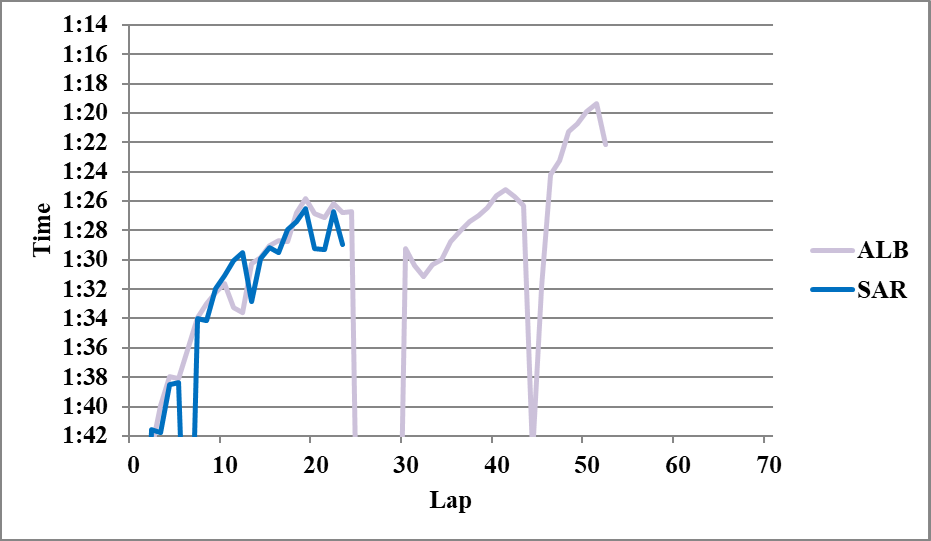
Writer: Takumi