1. 分析結果
タイヤ・燃料・ダーティエアや全力で走る必要性などの諸条件を考慮に入れると、レース全体でのペースの力関係について以下のことが言えた。
表1 ミディアムタイヤでのレースペース 1(第1スティント)
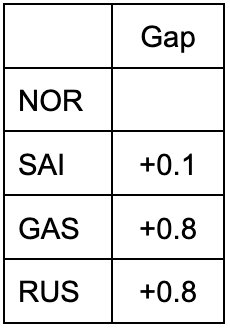
表2 ハードタイヤでのレースペース(第2スティント)
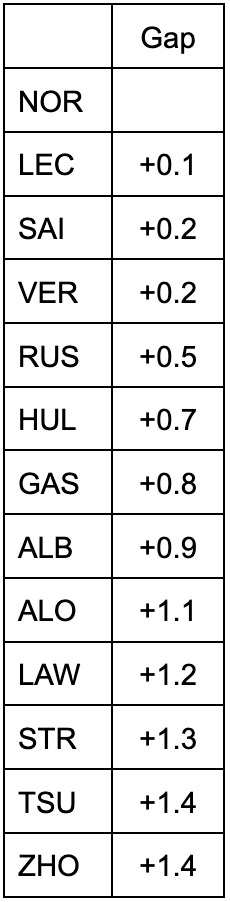
さらにこれらを総合すると、レース全体でのペースの力関係も以下のように理解することができるだろう。
表3 全体のレースペース

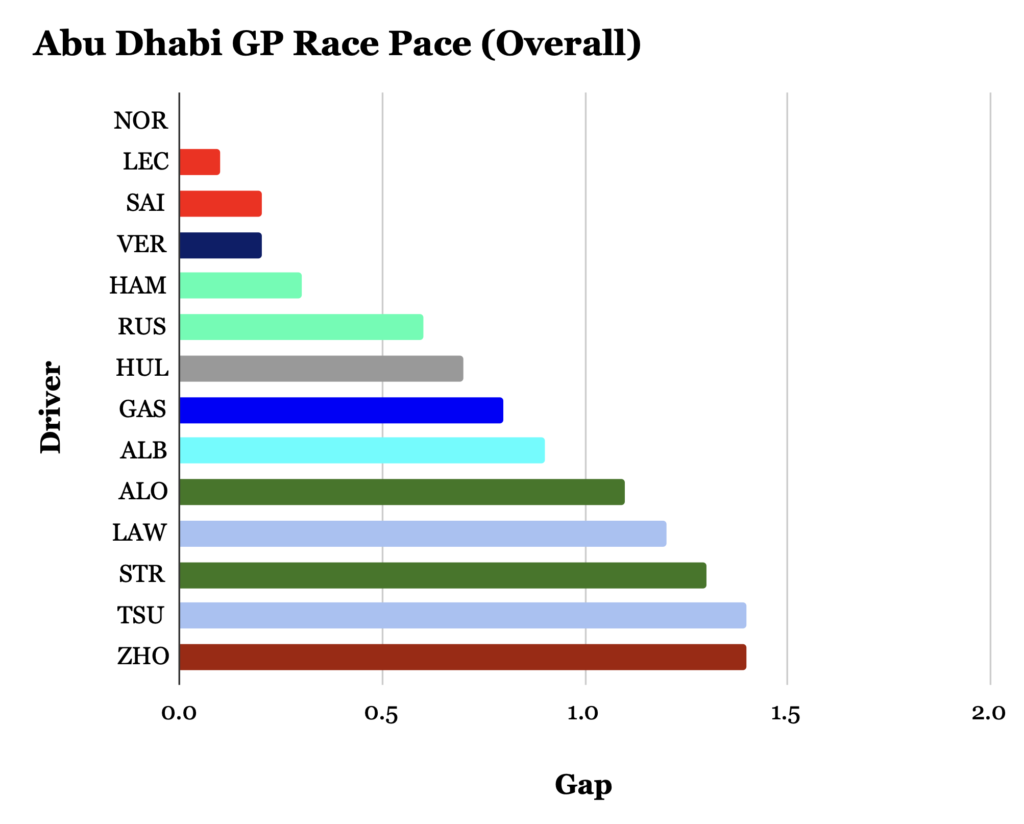
※注意点
リバースストラテジーを採ったハミルトンに関しては、ラッセルのペース比較を連立方程式を解く形で行った。レーストータルでのペース差において、ハミルトンが0.3秒速かったと結論づけ、それを表3に組み込んだ。
また、表1と表2を総合するにあたって、ノリスが両スティントで同じように力を発揮していたことを前提とした。
分析結果を振り返って
ノリスが最速のペースを示したが、フェラーリやレッドブルも接近しており、今年を象徴するようなレースペース勢力図となった。
ハミルトンは対ラッセルでは明確にアドバンテージを握り、マシンから全てを引き出した印象だが、それでもノリスのペースには及ばず、マシン自体はトップを争うにはあと一歩という点も、今季の象徴的な内容だった。
また、18番手スタートから入賞まであと一歩まで漕ぎ着けたアルボンのペースは非常に速く、かなり早めにピットに入ってライバル勢をアンダーカットしたにも関わらず、好ペースを維持した。終盤にはタイヤの温度を保てなくなってしまったようだが、非常に良いレースだった。
2. 分析方法について
フューエルエフェクトは0.06[s/lap]とし、グラフの傾きからデグラデーション値を算出。タイヤの履歴からイコールコンディションでのレースペースを導出した。計算方法については「4. 付録1」に記した。
また、クリア・ダーティエアやスティントの長さ、プッシュするインセンティブなどのレース文脈も考慮している。定量的に導出できないドライバーについては結論を出さず、信頼できる数字のみを公開する方針としている。
また、スティント前半でダーティエアでも、途中からクリアエアになっており、かつ前半のダーティエア内でもタイヤを労われていて極端なペースダウンでもない場合、スティント全体をクリアエアのように扱ってよいと考え、当サイトではその状態をオープンエンドクリアエア(OEC)と定義している。
また、分析対象はドライコンディションのみに限定している。
今回は予選で使用したソフトと新品ソフトの差、スクラブ済みと新品のミディアム・ハードの差は無視することとした。
3. 分析内容
下記に分析内容の一部を記す。
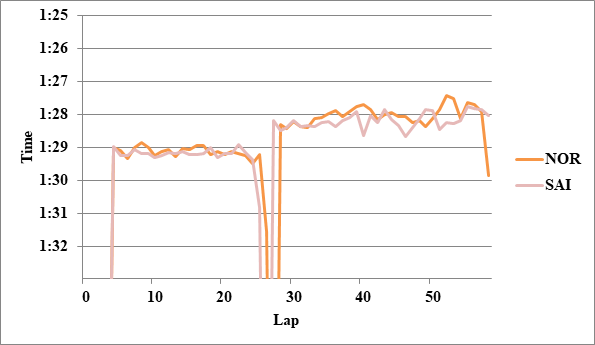
3.1. 第1スティントのノリスとサインツ
第1スティントでのペース比較は、基本的には、両者が自分のペースで走れるようになってからのラップタイムを単に平均したものになる。
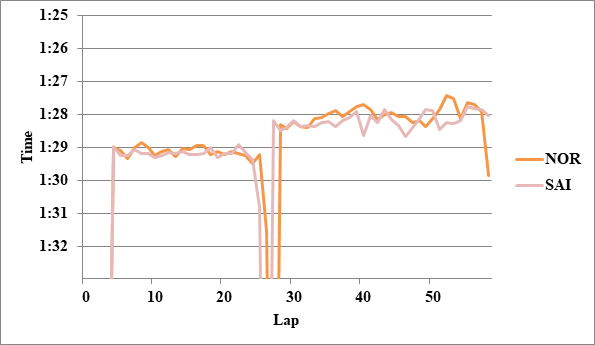
L4~24の平均で、ノリスが0.05秒速かった。ここでは四捨五入して0.1秒とする。
※注:ちなみに、リスタート直後に約3秒差から始まっているため四捨五入を採用したが、例えば1秒差から徐々に広がっていって2番手のドライバーがクリアエアになった場合は、2番手のドライバーがダーティエアでやや不利であることを考慮すると、0.05程度であれば切り捨てを採用する方が理にかなっている場合もある。
3.2. 第2スティントのノリスとサインツ
第2スティント以降ではタイヤの差を考慮する必要がある。一般的な計算式は「4. 付録1」に示したが、ここでは計算過程の一例として、ノリスとサインツの比較を行う。
まず第2スティントでは両者トラフィックでタイムが上下しているが、極端な(1秒以上ロスするような)ラップはなく、トラフィックは両者に平等だったと考えて、スティント全体すなわちL28からノリスがペースを落とす前のL57までを平均し、「ノリスはサインツより0.19秒速かった」を得た。これをΔTとする。
サインツは25周目、ノリスは26周目にピットに入り、デグラデーションはノリスが0.02[s/lap]、サインツが0.06[s/lap]、比較した区間はL27~57の31周。そして2人とも58周目を目指した。
よってサインツのスティントを通してのタイヤの不利C_tyreは、
C_tyre=0.06*1+(0.06-0.02)*31/2=0.68
そして、最終的な比較結果は「両者のスティント長の平均の長さのスティントを走った場合のペース差」で出すため、今回はそれは32.5周のスティントだ。その際にサインツが不利になる分C_stintを補正すると、
C_stint=(0.06-0.02)*32.5/2=0.65
よって、同じタイヤと燃料の状態で32.5周を走った場合のノリスのサインツに対する平均のペースアドバンテージは、
(最終的なペース差)=ΔT-C_tyre+C_stint=0.16
となり、四捨五入して「ノリスはサインツより0.2秒速かった」という結論を得る。
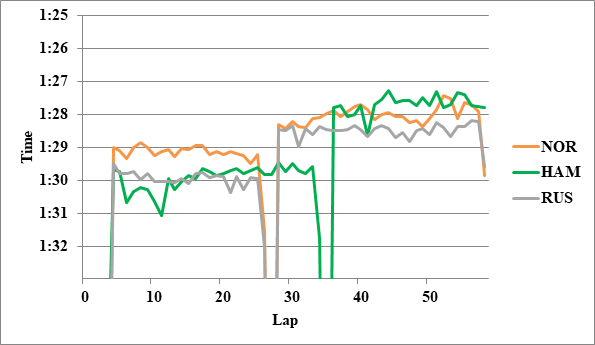
3.3. ハミルトンとラッセルの比較
今回のハミルトンはリバースストラテジーだったが、連立方程式を解く形でラッセルとのペース比較が可能だった。
まず図3にレースペースグラフを示す。
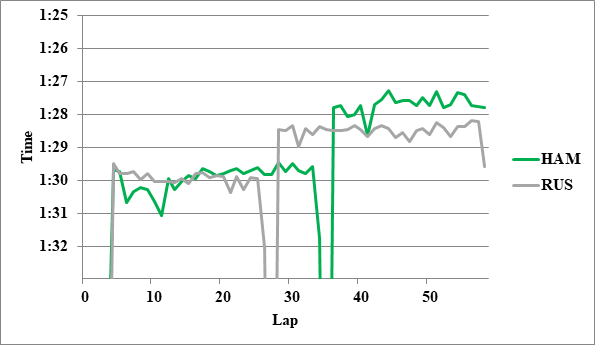
ハミルトンが第1スティントでT_1[s]、第2スティントでT_2[s]速かったとし、ミディアムタイヤのハードタイヤに対する優位性をT_M、両者の真の(イコールコンディションでの)ペース差をTと置くと、
T_1=T-T_M
T_2=T+T_M
となるため、
T=(T_1+T_2)/2
即ち、両スティントでのペース差を平均すれば求められることが分かる。
第1スティントでは、両者とも10周目過ぎまでダーティエアを走行してからクリアエアになるという同じ展開だったため、クリアエアになってからのペースを比較して良いと判断した。その結果ハミルトンが0.20秒速かった。
第2スティントでは、先ほどのノリスとサインツの比較と同じように比較を行い、ハミルトンが0.36秒速かったという結論を得た。
よって、平均するとハミルトンが0.28秒、四捨五入して0.3秒速かったと結論づけることができた。
3.4. その他の比較
同様にして以下の知見を得た。
「(第何スティントか):(速かった方のドライバー)>(もう一方のドライバー) タイム差」
の形式で示す。念のため、3.3までの内容も含めておく。
- HAM>RUS 0.3
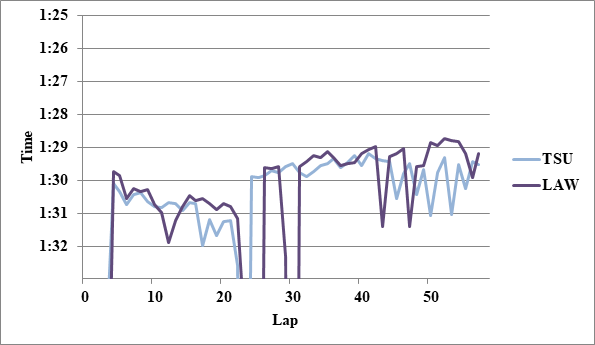
- 2: LAW>TSU 0.2
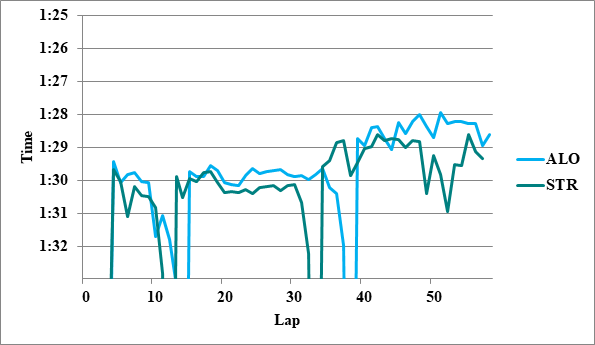
- 2: ALO>STR 0.2
- 1: NOR>SAI 0.1
- 2: NOR>SAI 0.2
- 1: NOR>RUS 0.8
- 2: NOR>RUS 0.5
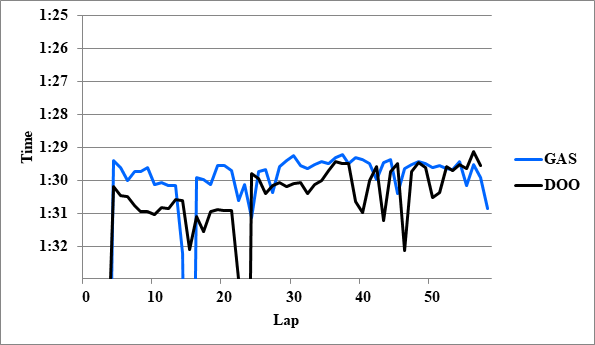
- 1: NOR>GAS 0.8
- 2: NOR>GAS 0.8
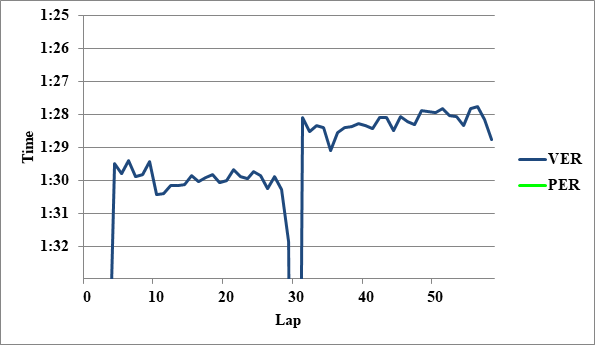
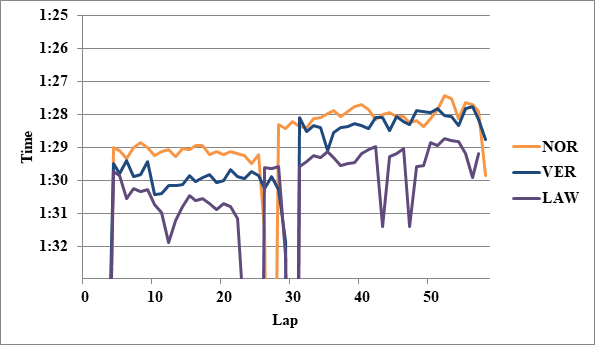
- 2: NOR>VER 0.2
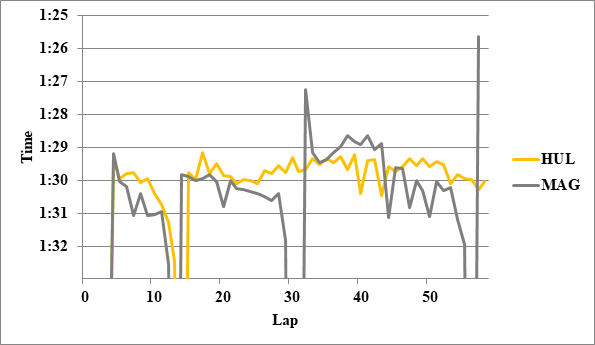
- 2: HUL>GAS 0.1
- 2: GAS>ALO 0.2
- 2: NOR>LAW 1.2
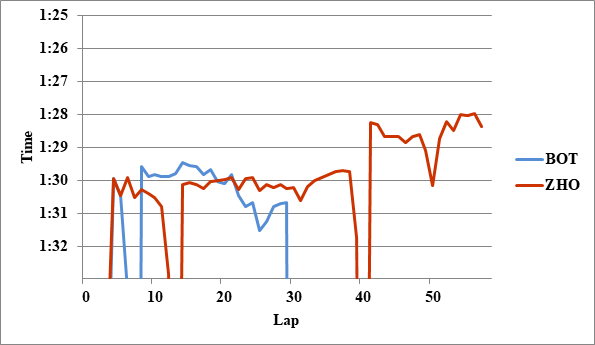
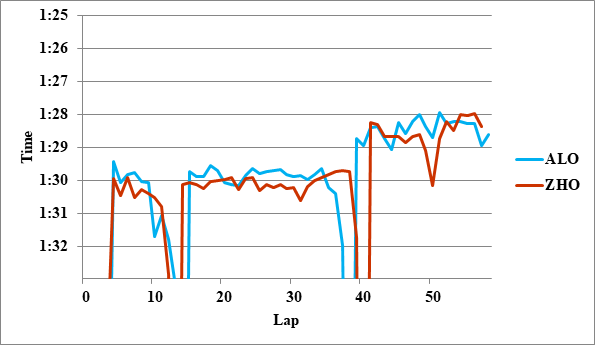
- 2: ALO>ZHO 0.3
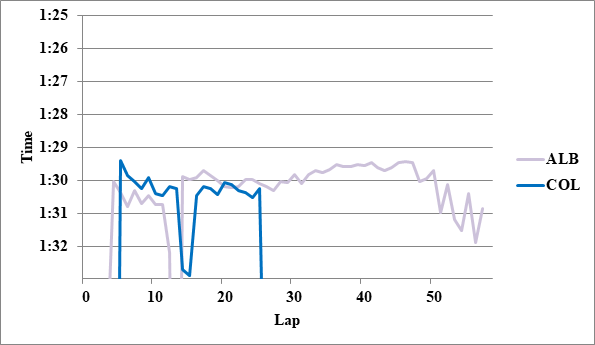
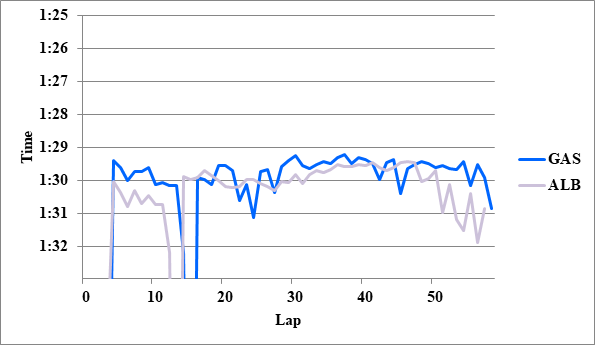
- 2: GAS>ALB 0.1
これらを総合し、1項で先に示した分析結果を得た。
4. 付録1
4.1. 両ドライバーのデグラデーションが一定の場合


4.2. デグラデーションが途中で変化する場合



5. 付録2
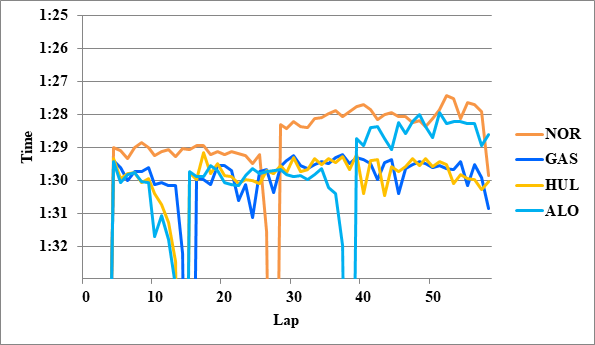
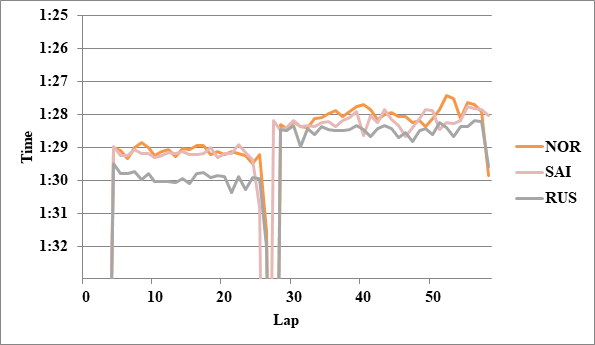
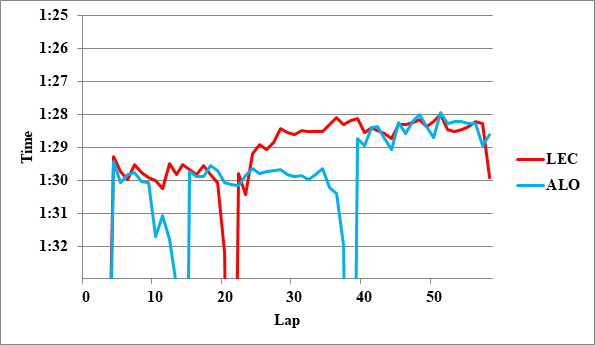
全チームのレースペースグラフ、および今回分析に使用したグラフを掲載する。
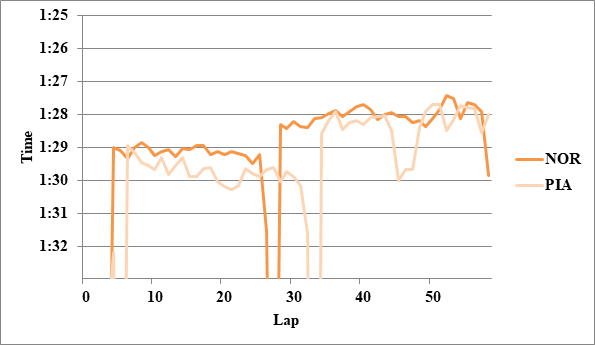
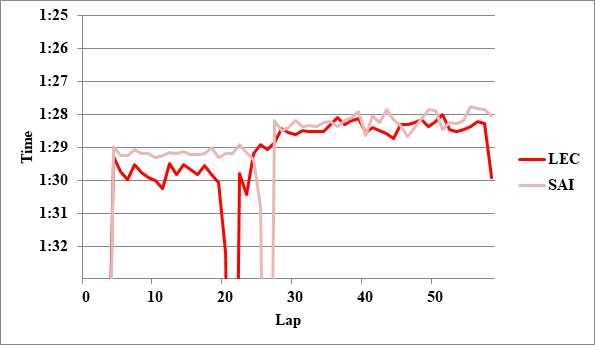
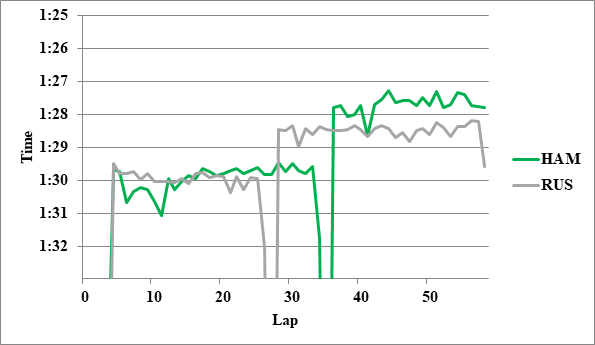
Writer: Takumi