1. 分析結果と結論
先に分析結果を示す。分析の過程については次項「レースペースの分析」をご覧いただきたい。
Table1 全体のレースペースの勢力図

※疑問符がつく部分はオレンジ色で示した
今回もハミルトンが圧倒的なレースペースを見せ、終盤戦を完全に制圧した。ハミルトンは、ボッタスに対してUSGPで0.4秒、ブラジルGPとサウジアラビアGPで0.5秒と、一貫して大差をつけており、いわゆる「マシンのおかげのチャンピオン」という一部からの心無い批判を腕でねじ伏せている。ボッタスとの差を見ても、昨年までのパフォーマンスレベルはまだ余力を残していたのではないか?と感じるほどだ。
結果はフェルスタッペンの戴冠となったが、ハミルトンも十分にチャンピオンに相応しい22戦の軌跡を歩んだと言える。互角のマシンと互角のドライバーが織りなす、歴史的なチャンピオンシップの目撃者となれたことに感謝しよう。
さて、中団勢ではアルファタウリとフェラーリが競争力を見せたが、ペース的には非常に接近しており、マクラーレンやアルピーヌの4チーム8台がどう入れ替わってもおかしくなかった。角田が今季初めてガスリーを上回り、サインツと並んで中団最速となったのも興味深い。
苦戦してしまったのはアストンマーティン。サウジアラビアに続き、競争力を欠いてしまった。その前のカタールでは中団トップ、メキシコでもそれに近いペースを見せていたことから、セットアップに気難しさのあるマシンなのかもしれない。
また今季何度か見られたように、シューマッハがラティフィと互角のペースを見せた。ソフトスタートで10周目ピットインとなってしまったため、苦しい戦略となったが、レース終盤もフレッシュなタイヤを履くラティフィを抑え続ける活躍を見せた。このシューマッハの好走がラティフィのクラッシュへと繋がり、周り回ってフェルスタッペンの初戴冠へと導かれる形となった。
注意点としては3つで、ペレスは燃料搭載量が少なかった場合、実力的にはあと0.3~0.4下だっただろう。またガスリーはミディアムとハードが同等という前提での数値だ。ただしこれはメルセデスでは実証されており、かけ離れてはいないだろう。そして、ノリスは第2スティント前半をクリーンエアと見なすか、微妙なところだ。
2. レースペースの分析
以下に分析の内容を示す。フューエルエフェクトは0.07[s/lap]で計算した。
また、各ドライバーのクリーンエアでの走行時を比較するために、全車の走行状態をこちらの記事にまとめた。
2.1 チームメイト同士の比較
最初にチームメイト同士の比較を見ていこう。
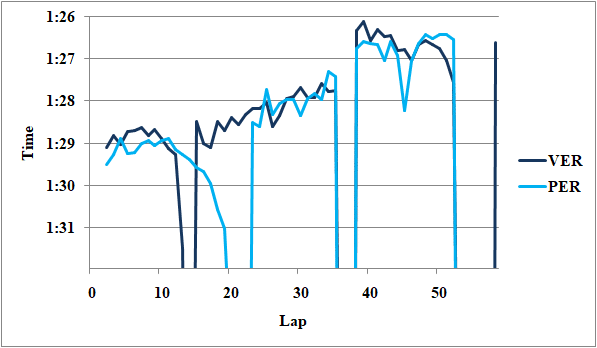
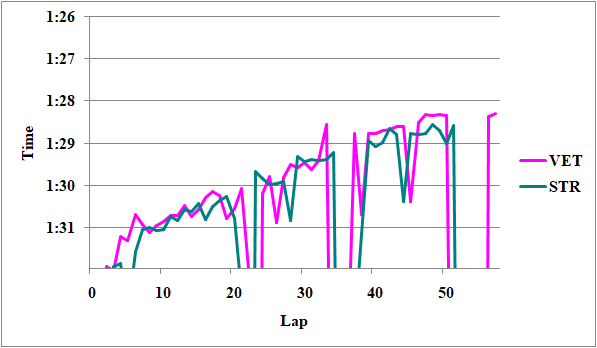
第1スティントでは、フェルスタッペンが0.2秒ほど上回っている。ただし、ペレスは長めのスティントを視野に入れて、よりマネジメントしていた可能性がある。
第2スティントではイーブンペースだ。ペレスのタイヤの方が8周新しいことを、デグラデーション0.02[s/lap]で考慮すると、実力的には0.2秒ほどフェルスタッペンが上回っていたと言える。
第3スティントでは同じタイヤで、フェルスタッペンが0.2秒上回っている。
総合すると、フェルスタッペンが綺麗に全てのスティントで0.2秒上回っていたことがわかる。
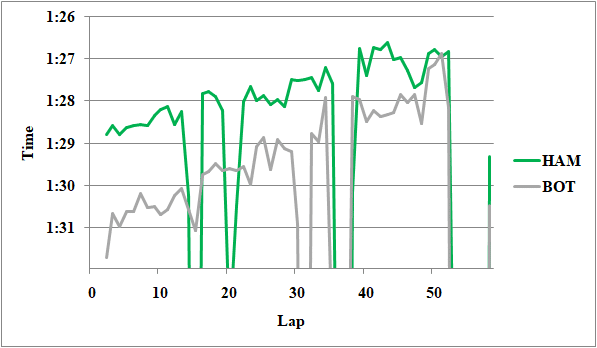
Fig.2 メルセデス勢のレースペース
タイヤが異なるが、ボッタスの第1スティント終盤はハミルトンの第2スティントの1.0秒落ちだ。ボッタスのタイヤの方が14周古いことを、デグラデーション0.03[s/lap]で考慮すると、実力的には0.6秒落ち程度と言える。
ハミルトンとエンジニアの無線のやり取りから、ミディアムとハードの差は僅かだったと考えられ、ひとまず疑問符付きでの答えとしよう。
一方で、第2スティント終盤で比較すると、ハミルトンが0.2秒ほど上回っている。ハミルトンのタイヤの方が16周古いことを、デグラデーション0.04[s/lap]として考慮すると、実力的には0.8秒程度と言える。さらにハミルトンがVSC前で温存していたことで0.1秒相当のタイヤのアドバンテージを作っていたことを加味すると0.7秒となる。り、レース前半の力関係と一致する。
ちなみにハミルトンのこのデグラデーション値は、VSC後は対フェルスタッペンでペースアップして、タイヤを酷使していた前提のものだ。50周目付近でペースが伸びきっていないのが、フェルスタッペンのペースを見てマネジメントに入っていた前提の場合は、デグラデーションを0.03[s/lap]とした上で50周目付近であと0.4秒速く走れたことになるので、ボッタスとの実力差は1.1秒となる。前述のミディアムでの力関係を鑑みても後者は考えにくく、ここからハミルトンはVSC後は終始かなりプッシュしていて50周目付近で余力は殆どなかったことが導けた。
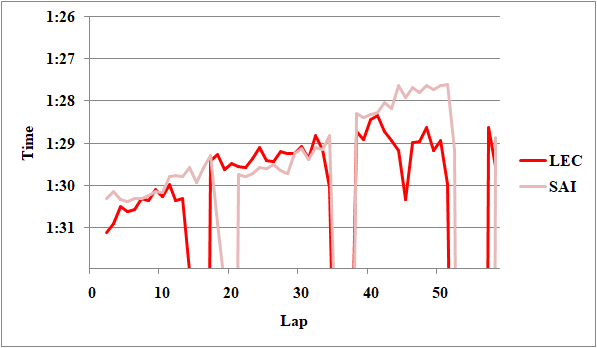
Fig.3 フェラーリ勢のレースペース
クリーンエアのタイミングが異なり、直接の比較はできない。
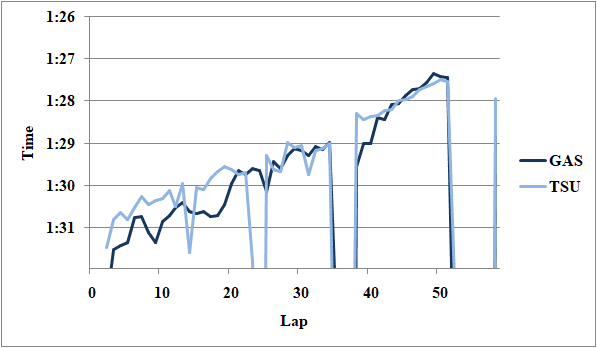
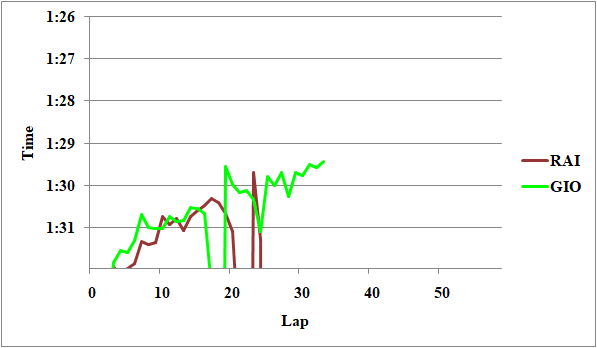
Fig.4 アルファタウリ勢のレースペース
タイヤは異なるが、第2スティントでハードのガスリーはミディアムの角田を平均0.1秒ほど上回っている。ガスリーのタイヤの方が13周新しい事を、デグラデーション0.01[s/lap]で考慮すると、有効数字の関係上切り上げて0.1秒ほど角田が上回っていたと言える。
ハミルトンとエンジニアの無線のやり取りから、ミディアムとハードの差は僅かだったと考えられ、疑問符付きでこれを両者の差と結論づけよう。
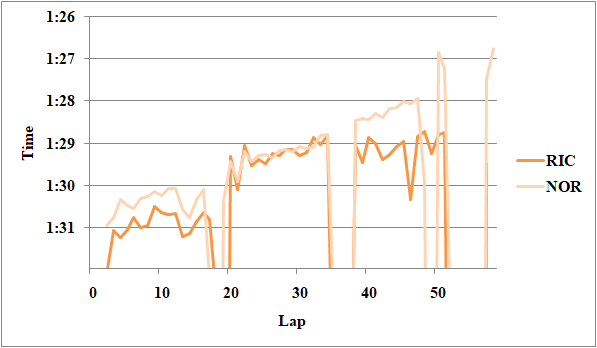
Fig.5 マクラーレン勢のレースペース
第2スティント前半で比較するとイーブンペースだ。デグラデーションは小さく、1周のタイヤの差は考慮しなくて良い。ただし第1スティントでは差がついていることからノリスの第2スティントのクリーンエアは、ガスリーの後ろでペースコントロールしているサインツに最小限のペースで追いつき、タイヤを労っていた可能性もある。よってやや疑問符付きの結論となる。
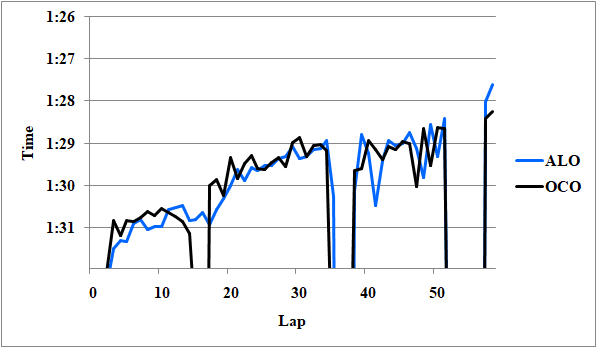
Fig.6 アルピーヌ勢のレースペース
アロンソの第1スティント後半とオコンの第2スティントで比較すると、オコンが0.1秒ほど上回っている。デグラデーションは0.00[s/lap]だが、18周のタイヤの差は有効数字の関係上、考慮する必要が無いとは言い切れない。デグラデーションが0.00[s/lap]の場合はオコンの0.1秒リード。0.01[s/lap]の場合は、アロンソが0.1秒リードということになる。ここでは仮に互角としておこう。
またアロンソの第2スティントはSC後に急激にペースアップしている点が気がかりだが、これも現段階では無視しておこう。
Fig.7 アストンマーティン勢のレースペース
第2スティント後半で比較すると、ベッテルが0.2秒ほど上回っている。ベッテルのタイヤの方が2周新しいことを、デグラデーション0.03[s/lap]で考慮すると、実力的には0.1秒程度と言える。
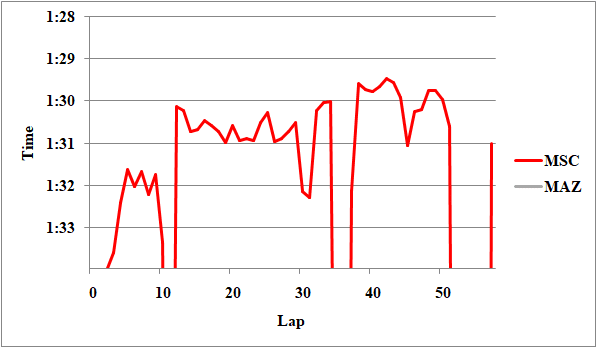
Fig.8 ハース勢のレースペース
比較可能なデータはなし。
Fig.9 ウィリアムズ勢のレースペース
定量的な比較はできないが、定性的にはラッセルの方が速かったと考えられる。
Fig.10 アルファロメオ勢のレースペース
比較可能なデータはなし。
2.2 ライバルチーム同士の比較
続いて、チームを跨いだ比較を行う。
2.2.1 第2スティントでハードを履いたドライバーなど
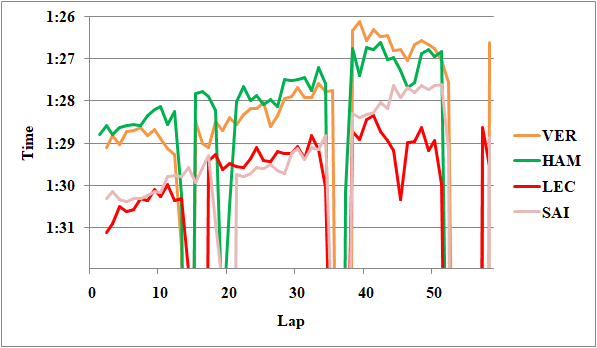
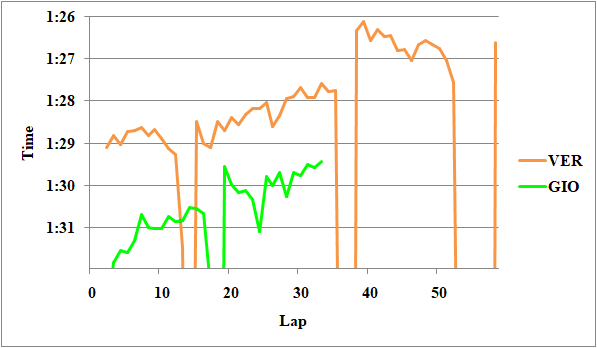
まず、図1にフェルスタッペン、ハミルトン、ルクレール、サインツの比較を示す。
Fig.11 フェルスタッペン、ハミルトン、ルクレール、サインツのレースペース
まずはフェルスタッペンとハミルトンの比較だ。第2スティントに着目すると、VSC前でのハミルトンのペースはフェルスタッペンを平均0.24秒上回っている。ちなみにデグラデーションが0.02[s/lap]のため、1周のタイヤの差を考慮すると、ハードタイヤでの実力差は0.2秒程度だったと言える。
VSC後では、フェルスタッペンのペースはハミルトンを0.3秒ほど上回っている。フェルスタッペンのタイヤが22周分新しいことを考慮すると、実力的にはハミルトンの方が0.4秒速かったことになる。
平均して0.3秒をこのレースでのパフォーマンス差としよう。
ちなみに第1スティントはダーティエアの影響もあるため、評価しづらいが、同じような数値と考えられ、頷ける。
チームメイト比較で、ハミルトンとボッタスの第1スティントでの差は0.6秒だったが、上記の考察内容より、VSC前のハミルトンが0.1秒余裕を持って走っていると考えられるため、2人の差は0.7秒となる。これは第2スティントでの差と全く同じだ。チームメイト比較時は、16周のタイヤの差により有効数字上やや疑問符が生じていたが、上述の疑問符と合わせて辻褄があっており、打ち消し合う形で0.7秒を結論として良いだろう。
続いてルクレールを見てみよう。第2スティント前半をクリーンエアと見なすならば、フェルスタッペンの1.2秒落ちのペースだ。デグラデーションが十分に小さいため2周のタイヤ履歴の差は考慮しなくて良い。
サインツは、VSC後でハミルトンの1.2秒落ちのペースだ。前述の通りハミルトンが履いていた0.1秒の下駄と、サインツのタイヤの方が6周新しいことを、デグラデーション0.03[s/lap]で考慮すると、ハミルトンの1.3秒落ちと言える。
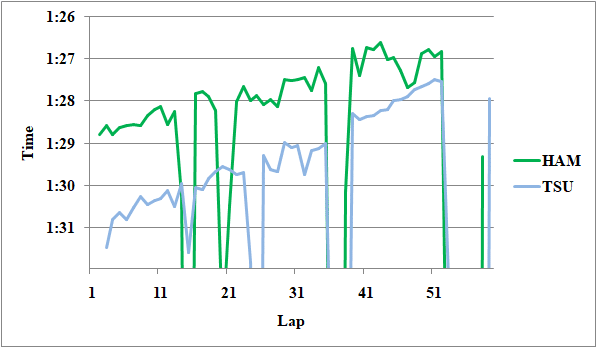
続いてハミルトンと角田を比較する。
Fig.12 ハミルトンと角田のレースペース
角田のVSC後はハミルトンの1.1秒落ちだ。また前述の通り、ハミルトンはここではレース全体でのパフォーマンスレベルより0.1秒速く走っている。
角田のタイヤの方が9周新しいことを、デグラデーション0.01[s/lap]で考慮すると、実力的にはハミルトンの1.3秒落ちと言える。
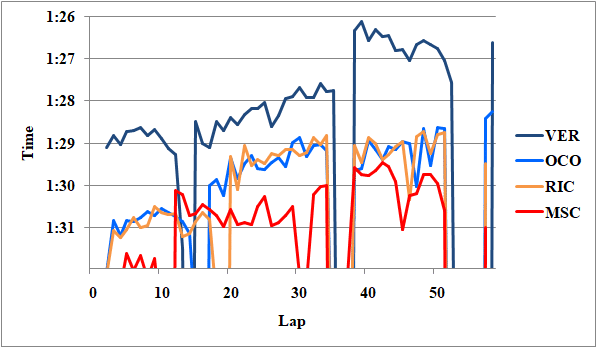
続いてオコンとリカルド、シューマッハの第2スティントをフェルスタッペンと比較しよう。
Fig.13 フェルスタッペン、オコン、リカルド、シューマッハのレースペース
オコンは、第2スティント前半でフェルスタッペンの1.3秒落ちだ。オコンのタイヤの方が2周新しいことは、デグラデーションが十分に小さいため考慮しなくて良い。
リカルドは、第2スティント前半でフェルスタッペンの1.2秒落ちだ。リカルドのタイヤの方が5周新しいことを、デグラデーション0.02[s/lap]で考慮すると、実力的には1.3秒落ちとなる。
シューマッハは、第2スティント前半でフェルスタッペンの2.5秒落ちだ。シューマッハのタイヤの方が3周古いことをデグラデーション0.07[s/lap]で考慮すると、実力的には2.3秒落ちと言える。
次に、サンプルが少ないものの、同様にジョビナッツィもフェルスタッペンと比較してみよう。
Fig.14 フェルスタッペンとジョビナッツィのレースペース
ジョビナッツィはクリーンエアとなった29周目以降では、フェルスタッペンの1.8秒落ちだ。ジョビナッツィのタイヤの方が4周新しいことを、デグラデーション0.02[s/lap]で考慮すると、実力的には1.9秒落ちと言える。
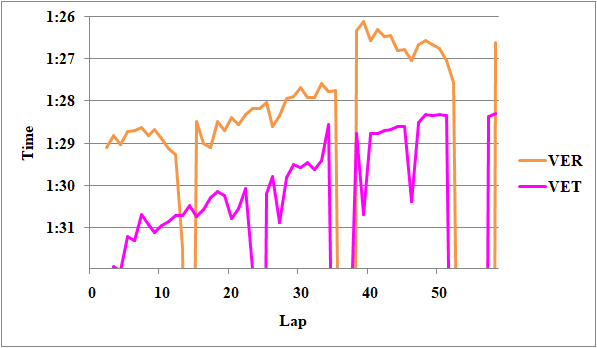
続いてベッテルのVSC後をフェルスタッペンと比較してみよう。
Fig.15 フェルスタッペンとベッテルのレースペース
ベッテルのペースはフェルスタッペンの2.1秒落ち程度だ。ベッテルのタイヤの方が13周古いことを、デグラデーション0.03[s/lap]で考慮すると、フェルスタッペンの1.7秒落ちと言える。
2.2.2 ハードスタート組を紐解く
ここからはハードでスタートしたガスリーとアロンソを、2.1の分析結果の中に組み込むべく、分析してみよう。
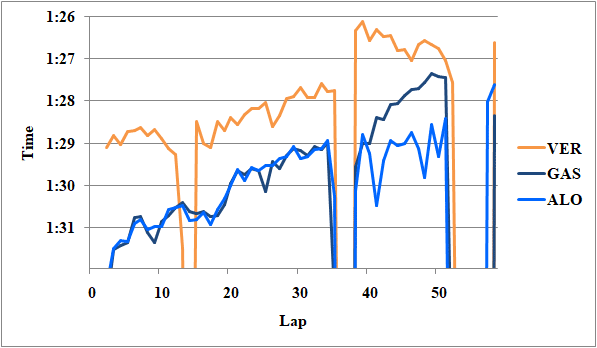
図16にフェルスタッペン、ガスリー、アロンソのレースペースを示す。
Fig.16 フェルスタッペン、ガスリー、アロンソのレースペース
まずアロンソの第1スティントは、フェルスタッペンのハードタイヤの第2スティントのペースの1.4秒落ち程度だ。デグラデーションは評価しづらいが、0.00[s/lap]とするならば1.4秒落ち。0.01[s/lap]とするならば1.3秒落ちだ。
チームメイト比較でのオコンと同等との結論を鑑みつつ、いくらペースを抑えていても13周でタイヤのタレが0.0秒とは考えにくいことから、フェルスタッペンの1.3秒落ちを採用しよう。
一方VSC後、ミディアムタイヤに履き替えたアロンソはガスリーの1.0秒落ちだ。アロンソの競争力がハードとミディアムで変わらないと仮定すれば、ガスリーはフェルスタッペンの0.3秒落ちで、ボッタス以上、ペレスに近い競争力を有していたことになるが、それは考えにくい。また、そこまで速ければ第1スティントでアロンソをオーバーテイクしていたはずだ。したがって、アロンソがミディアムに履き替えてから競争力を落としたのは間違いない。
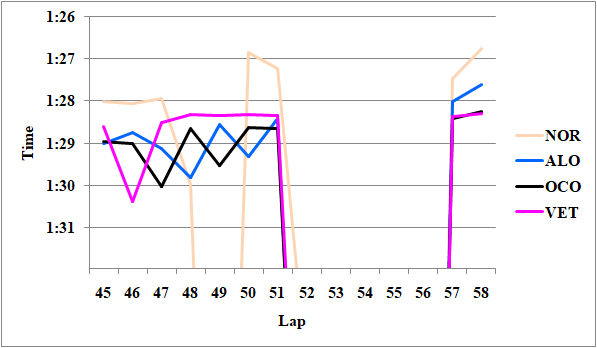
しかし、これは非常に解釈が難しい。何故ならば図17に示す通り、SCの追い越しを許可された、ノリス、アロンソ、オコン、ルクレール、ベッテルの中で、SC前までクリーンエアで走っていたノリスやベッテルはラスト2周でSC前と互角のタイムしか出せておらず、アロンソに前を抑えられていたオコンですら、0.3秒程度のタイムアップに止まっている中で、アロンソが0.6秒のタイムアップを果たしているからだ。
Fig.17 ノリス、アロンソ、オコン、ベッテルのレース終盤のペース
チーム別分析ではミディアムとハードが互角の性能という前提で、ガスリーを角田の0.1秒落ちとしたが、この前提だとハードタイヤのアロンソを0.2秒上回っていることになる。そしてミディアムで1.0秒上回ったアロンソは0.6秒余裕を持っていた、と考えればミディアムでの差が0.4秒となり、ハードタイヤの勢力図からはかけ離れはしない。
しかし、ここで出てくる問題は、アロンソにとって0.6秒余裕を持って走るメリットが無いことだ。事実、角田やガスリーに交わされてしまっており、プッシュしていれば可能だった4位フィニッシュをミスミス逃したことになる。
したがって、最も考えられるのはピットアウト後に角田とバトルした際に、タイヤに負荷を掛け、強力なサーマルデグラデーションを引き起こした可能性だ。これがスローペースの原因となり、SC中に冷やせたことで0.6秒のゲインに繋がったのではないだろうか?
よって、ここではアロンソのペースの実力的な真値はハードタイヤを基準としたフェルスタッペンの1.3秒落ち、ガスリーのペースはチームメイト比較で導いた角田の0.1秒落ちを結論としたい。
2.2.3 ラティフィのペース
ミディアムスタートのラティフィはボッタスと比較するのが妥当だろう。
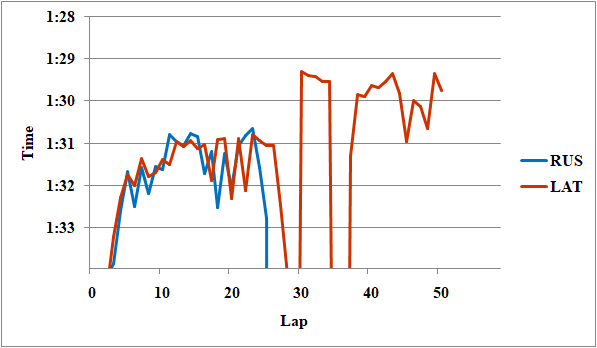
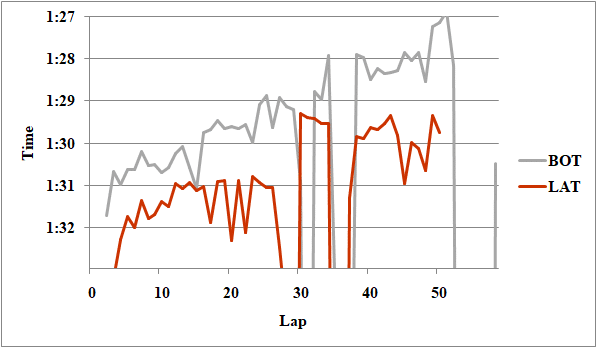
Fig.18 ボッタスとラティフィのレースペース
ラティフィはボッタスの1.9秒落ちとなっている。タイヤは同様だ。
以上、2.2.1、2.2.2と2.2.3の結果を総合すると、前述の表1の結果になる。